10444
Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия α-частицы E_min = 8 МэВ.

10451
Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.

10452
Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l находится в возбужденном состоянии (n = 3). Определить, в каких точках интервала 0 < х < l плотность вероятности нахождения частицы имеет максимальное и минимальное значения.

10458
Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале 0 < х < l плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.

10444
Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия α-частицы E_min = 8 МэВ.

10454
Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность w обнаружения частицы в крайней четверти ящика?

14261
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, х₂) обнаружения частицы в интервале от x₁ = 0,3l до x₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14293
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 73,72. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,2l до х₂ = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14306
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 51,19 эВ. Найти квантовое число n, характеризуются энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,2l до x₂ = 0,3l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14364
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 2,048 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, x₂) обнаружения частицы в интервале от x₁ = 0,3l до х₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14365
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 2,048 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, x₂) обнаружения частицы в интервале от x₁ = 0,4l до х₂ = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14381
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной ямс шириной l = 10^–10 м. Энергия частицы W_n = 37,63 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, х₂) обнаружения частицы в интервале от x₁ = 0,2l до х₂ = 0,3l. Построить график зависимости от координаты х плотности вероятности |ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14580
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 73,72 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, x₂) обнаружения частицы в интервале от x₁ = 0,3l до x₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14968
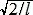
Одномерная нормированная волновая функция ψ(x) = ·sin(πx/l) описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность w нахождения такой частицы вблизи стенки ящика, то есть когда 0 ≤ x ≤ 0,01l.

14969
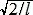
Одномерная нормированная волновая функция ψ(x) = ·sin(πx/l) описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить отношение θ вероятности нахождения такой частицы в первой трети ящика (0 < х < l/3) к вероятности нахождения в последней трети (2l/3 ≤ ν ≤ l).

14970
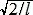
Одномерная нормированная волновая функция ψ(x) = ·sin(πx/l) описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность w нахождения такой частицы в средней части ящика, то есть когда l/2–0,01l ≤ x ≤ l/2+0,01l.

15949
Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Найти отношение разности ΔЕ_n, _n+1 соседних энергетических уровней к энергии Е_n частицы в трех случаях: 1) n = 2; 2) n = 5; 3) n → ∞.

16605
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 73,72. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,4l до х₂ = 0,5l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16610
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,2l до x₂ = 0,3l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16611
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,3l до x₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16612
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 32,76 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,4l до x₂ = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16613
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 8,191 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, x₂) обнаружения частицы в интервале от x₁ = 0,3l до х₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16614
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 8,191 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, x₂) обнаружения частицы в интервале от x₁ = 0,4l до х₂ = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16615
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 51,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,4l до x₂ = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16616
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 61,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,3l до x₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16618
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 51,19 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,3l до x₂ = 0,4l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16622
Частица протон с энергией E_n = 51,19 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,2l до х₂ = 0,4l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16623
Частица протон с энергией E_n = 32,76 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,2l до х₂ = 0,3l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16626
Частица протон с энергией E_n = 18,43 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,4l до х₂ = 0,5l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16628
Частица протон с энергией E_n = 2,048 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,6l до х₂ = 0,9l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16693
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁,х₂) обнаружения частицы в интервале от х₁ = 0,3l до х₂ = 0,4l. Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

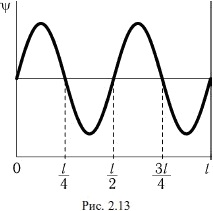
19182
Частица находится в одномерном потенциальном ящике с бесконечно высокими стенками. Пси-функция имеет вид, показанный на рисунке 2.13. Найти вероятность пребывания частицы в области l/8 < х < l/2.

19183
Частица находится в основном состоянии в одномерной бесконечно глубокой потенциальной яме. Какова вероятность нахождения частицы в средней трети ящика.

19499
Определить вероятность обнаружения частицы в первой трети одномерного прямоугольного "потенциального ящика" шириной l с бесконечно высокими "стенками", если частица находится в основном состоянии.

21829
Электрон движется в одномерной бесконечно глубокой потенциальной яме шириной 0,6 нм, имея энергию 16,6 эВ. Какова вероятность обнаружения этого электрона в первой четверти ямы?