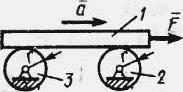13126
Выведите формулу для момента инерции цилиндрической муфты относительно оси, совпадающей с ее осью симметрии. Масса муфты равна m, внутренний радиус r, внешний R.

11139
Вычислить момент инерции J проволочного прямоугольника со сторонами а = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ = 0,1 кг/м.

11145
Определить момент инерции J кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной к кольцу.

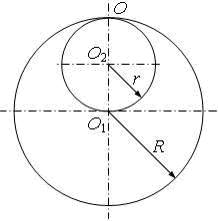
11345
Из тонкого однородного диска радиусом R = 20 см вырезана часть, имеющая вид круга радиусом r = 10 см, так, как это показано на рисунке. Оставшаяся часть диска колеблется относительно горизонтальной оси О, совпадающей с одной из образующих цилиндрической поверхности диска. Найти период Т колебаний такого маятника.

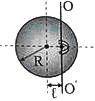
26448
Определить момент инерции шара массой 10 кг и радиусом 20 см относительно оси, расположенной на расстоянии l = 0,5R от центра шара.

26448
Определить момент инерции шара массой 10 кг и радиусом 20 см относительно оси, расположенной на расстоянии l = 0,5R от центра шара.

23983
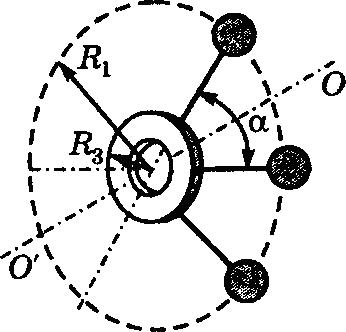
Определите момент инерции стального маховика относительно оси вала. Плотность стали ρ = 7800 кг/м³, радиус центрального отверстия для вала r = 0,1 м, R₁ = 6r, R₂ = 4r, R₃ = 2r, α = 45°. Плоский маховик толщиной h = 0,02 м с цилиндрическими вырезами. Количество вырезов n найдите по формуле n = 360/α, их радиусы равны r.

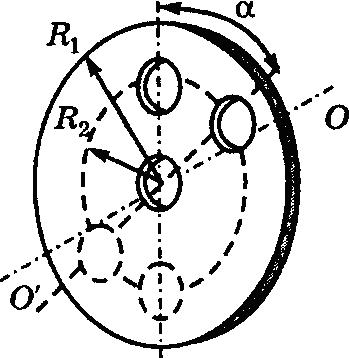
26575
Определите момент инерции стального маховика относительно оси вала. Плотность стали ρ = 7800 кг/м³, радиус центрального отверстия для вала r = 0,1 м, R₁ = 6r, R₂ = 4r, R₃ = 2r, α = 180°. Маховик с шарами на спицах. Количество шаров п найдите по формуле n = 360/α, их радиусы равны r, длина втулки равна 0,02 м. Массами спиц пренебречь.

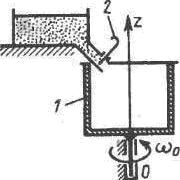
26599
Резервуар 1, момент инерции которого относительно вертикальной оси Oz равен 1 кг·м², вращается с угловой скоростью ω₀ = 18 рад/с. После открытия задвижки 2 он заполняется сыпучим материалом. Определить угловую скорость заполненного резервуара, если его момент инерции равен 3 кг·м².

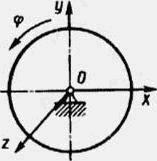
26617
Диск вращается вокруг оси Oz по закону φ = t³. Определить модуль момента пары сил, приложенной к диску, в момент времени t = 1 с, если момент инерции диска относительно оси вращения равен 2 кг·м².

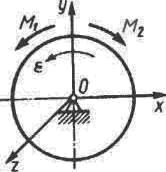
26618
Диск вращается вокруг центральной оси с угловым ускорением ε = 4 рад/с² под действием пары сил с моментом M₁ и момента сил сопротивления М₂ = 6 Н·м. Определить модуль момента М₁ пары сил, если момент инерции диска относительно оси вращения равен 6 кг·м².

26624
Балка 1 массой m₁ = 200 кг лежит на валах 2 и 3, моменты инерции которых относительно оси вращения I₁ = I₂ = 0,1 кг·м². Определить силу F, которую необходимо приложить к балке, чтобы сообщить ей ускорение а = 1 м/с², если радиус r = 0,1 м.

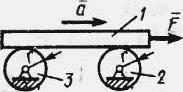
12946
Определить момент инерции кольца массой m = 250 г и радиусом R = 10 см относительно оси, касательной к кольцу.

13640
Выведите формулу для момента инерции тонкого кольца радиусом R и массой m относительно оси симметрии.

13641
Выведите формулу для момента инерции тонкого стержня массой m и длиной l относительно оси, проходящей через центр масс перпендикулярно его длине.

14991
К ободу однородного сплошного диска диаметром 90 см приложена постоянная касательная сила 0,1 кН, приводящая к вращению диска относительно оси, проходящей через его центр инерции. При вращении диска на него действует еще и момент сил трения величиной 20 Н·м. За 5 с диск увеличивает свою частоту вращения со 180 до 300 об/мин. Определить массу диска.

15049
Найти момент инерции полого цилиндра радиусами R₁ и R₂ и массой m относительно оси симметрии цилиндра.

15050
Найти момент инерции конуса массой m и радиусом основания R относительно оси симметрии конуса.

15465
Локомотив приводится в движение турбиной, ось которой параллельна осям колес. Направление вращения турбины совпадает с направлением вращения колес. Момент инерции ротора турбины относительно собственной оси I = 240 кг·м². Найти добавочную силу давления на рельсы, обусловленную гироскопическими силами, когда локомотив идет по закруглению радиуса R = 250 м со скоростью v = 50 км/ч. Расстояние между рельсами l = 1,5 м. Турбина делает n = 1500 об/мин.

15467
Корабль движется со скоростью v = 36 км/ч по дуге радиусом R = 200 м. Найдите момент гироскопических сил, действующих на подшипник со стороны вала с маховиком, которые имеют момент инерции относительно оси вращения J = 3,8·10³ кг·м² и делают n = 300 об/мин. Ось вращения ориентирована вдоль корабля.

16536
Как изменится момент инерции свинцового цилиндра относительно его оси, если его сплющить в диск, толщина которого стала меньше высоты цилиндра в 10 раз?

17476
Найдите момент инерции J и момент количества движения L земного шара относительно оси вращения, если принять Землю за однородный шар массой М и радиусом R. Период вращения Земли Т.

17477
Найти момент инерции и момент импульса земного шара относительно оси вращения, если принять Землю за однородный шар массой m = 5,96·10²⁴ кг и радиусом R = 6,37·10⁶ м.

17670
Диск (m = 50 кг, R = 60 см) вращается относительно неподвижной оси. Угол поворота зависит от времени по закону φ = 2t + 0,5t² (рад). Найти сумму проекций моментов сил на данную ось.

17987
Полый цилиндр вращается относительно оси, совпадающей с осью цилиндра. Закон вращения имеет вид φ = 10 – 5t + 0,5t ². Определить момент инерции и массу цилиндра, если его радиус 0,05 м. Момент силы относительно оси вращения, действующий на цилиндр, 0,75 Н·м.

19505
Определить момент инерции диска радиусом R = 30 см с центральным отверстием радиусом r = 10 см относительно оси симметрии. Масса диска m = 4 кг.

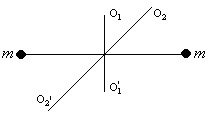
20735
Две материальные точки массами m расположены симметрично относительно оси O₁O₁', расположенной в плоскости чертежа. Как изменится момент инерции этих точек при повороте оси в плоскости чертежа на угол α = 45° из положения O₁O₁' в положение O₂O₂'.

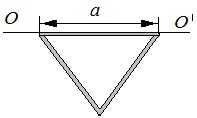
20737
Определите момент инерции проволочного равностороннего треугольника со стороной а = 10 см относительно оси, совпадающей с одной из сторон треугольника. Масса треугольника равна m = 12 г и равномерно распределена по длине проволоки.

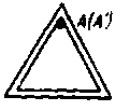
21317
Одно или несколько тел (цилиндры, шары, диски, обручи) радиусом r и массой m₁ подвешены в точке А или закреплены на стержнях массой m₂ = 100 г, длина которых l = 40 см значительно превышает их толщину. Найти моменты инерции J систем тел относительно заданной оси АА'. Выполнить дополнительное задание.

21659
Полый цилиндр массой 8 кг имеет внутренний диаметр 1 м, внешний 1,1 м. Чему равен момент инерции этого цилиндра относительно своей оси?

21948
Шарик радиуса 6,2 см из пластичного материала имеет некоторый момент инерции I₁. Этот шарик преобразуют в цилиндр высоты 3,8 см. Момент инерции цилиндра относительно его оси оказался I₂. Найти отношение I₂/I₁.

23415
Тело массой m = 4 кг, закрепленное на горизонтальной оси, совершало колебания с периодом T₁ = 0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период T₂ колебаний стал равным 1,2 с. Радиус R диска равен 20 см, масса его равна массе тела. Найти момент инерции J тела относительно оси колебаний.

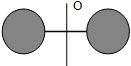
23997
На рисунке схематично изображена молекула кислорода. Момент инерции молекулы кислорода относительно оси О равен 19,2·10^–40 г·см³. Определить значение средней квадратичной частоты вращения молекулы кислорода при 27 °С относительно оси О.

24051
Чему равен момент инерции диска I радиусом r относительно оси ОО, когда из него вырезали диск радиусом r/2. Толщина диска b, плотность ρ.

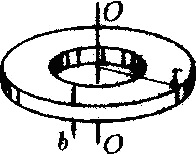
24143
Вал радиусом 8 см и массой 40 кг относительно оси АА' имеет момент инерции (в кг·м²):

26547
Горизонтальный диск вращается вокруг вертикальной оси с угловой скоростью ω₁; его момент инерции относительно оси вращения J₁. На него падает другой диск с моментом инерции относительно той же оси J₂ и угловой скоростью ω₂. Плоскости дисков параллельны, центры — на одной вертикальной линии. Нижняя поверхность падающего диска снабжена шипами, которые впиваются в верхнюю поверхность нижнего диска и скрепляют диски в одно целое. а) Найти угловую скорость ω получившейся системы. б) На сколько изменится общая кинетическая энергия обоих дисков после падения второго диска? в) Чем объяснить изменение общей кинетической энергии дисков?