10074
Определить частоту ν простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

60512
Определить потенциал поля, образованного диполем, в точках плоскости, перпендикулярной его оси и проходящей через середину отрезка, соединяющего заряды диполя.

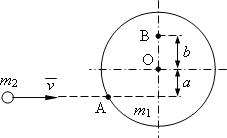
25905
Однородный диск массой m₁ = 0,2 кг может свободно вращаться вокруг горизонтальной оси z, перпендикулярной плоскости диска и проходящей через точку О. В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью v = 10м/с и прилипает к его поверхности. Масса шарика равна m₂ = 10 г. Определить угловую скорость ω диска и линейную скорость u точки В на диске в начальный момент времени. Вычисления выполнить для следующих случаев: 1) a = R, b = R; 2) a = R/2, b = R; 3) a = 2/3R, b = R/2; 4) a = 1/3R, b = 2/3R. Радиус R диска равен 20 см.

14647
Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу А надо совершить, чтобы остановить диск?

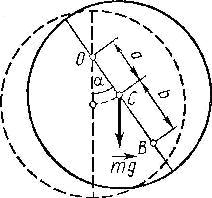
11151
Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем. Диск отклонили на угол α и отпустили. Определить для начального момента времени угловое ε и тангенциальное а_τ ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: 1) a = R, b = R/2, α = π/2; 2) a = R/2, b = R, α = π/6; 3) a = 2/3R, b = 2/3R, α = 2/3π.

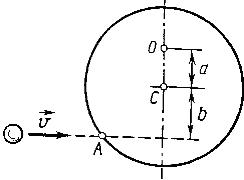
11161
Однородный диск массой m₁ = 0,2 кг и радиусом R = 20 см может свободно вращаться вокруг горизонтальной оси z, перпендикулярной плоскости диска и проходящей через точку С. В точку, А на образующей диска попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью v = 10 м/с, и прилипает к его поверхности. Масса m₂ шарика равна 10 г. Определить угловую скорость ω диска и линейную скорость u точки О на диске в начальный момент времени. Вычисления выполнить для следующих значений а и b: 1) a = b = R; 2) a = R/2,b = R; 3) a = 2R/3, b = R/2; 4) a = R/3, b = 2R/3.

11344
Диск радиусом R = 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину L и период Т колебаний такого маятника.

26696
Сплошной однородный диск радиусом R = 0,1 m колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска. Какой длины должен быть математический маятник, имеющий тот же период колебаний, что и диск?

11817
В однородном магнитном поле с индукцией B = 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной l = 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения n = 16 с^-1.

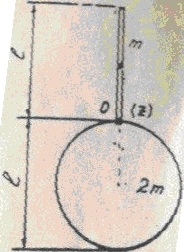
12053
Определить циклическую частоту ω гармонических колебаний физического маятника, состоящего из однородного стержня длины l = 1 м и однородного плоского диска, укрепленного на стержне так, как его показано на рисунке. Масса стержня равна m, масса диска 2т. Горизонтальная ось z проходит через точку O перпендикулярно плоскости диска.

13436
Прямолинейный проводник длиной L = 1,5 м находится в однородном магнитном поле с индукцией В = 1 Тл. Проводник вращается в плоскости, перпендикулярной линиям индукции поля, со скоростью (150/π) (об/с). Определите разность потенциалов на концах проводника как функцию расстояния оси его вращения от одного из концов проводника и вычислите разность потенциалов, если ось вращения проходит: а) через один из концов проводника; б) через середину проводника; в) на расстоянии (1/4) его длины от одного из концов.

13506
Тонкое кольцо радиусом R = 10 см несет заряд Q = 10 нКл. Кольцо равномерно вращается с частотой n = 10 (об/с) относительно оси, перпендикулярной плоскости кольца и проходящей через центр кольца. Найти магнитный момент p_m кругового тока, создаваемого кольцом.

14000
Определить период T гармонических колебаний физического маятника, состоящего из однородного стержня длины l = 1 м и обруча, скрепленного со стержнем так, как это показано на рисунке. Масса стержня равна 3m, масса обруча 2m. Горизонтальная ось Oz проходит через точку O перпендикулярно плоскости обруча.

19917
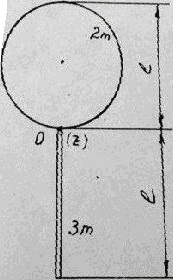
Диск радиусом 10 см и массой 2 кг вращается вокруг оси, проходящей перпендикулярно его плоскости через середину радиуса. Закон движения диска φ = 6 + 4t – t² (рад). Определить момент силы, действующей на диск, и кинетическую энергию диска через 2 с после начала вращения диска. Построить график зависимости момента силы и момента импульса диска от времени.

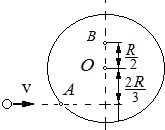
20744
Однородный диск радиусом R = 20 см и массой m₁ = 0,20 кг может свободно вращаться вокруг неподвижной горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем. В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально со скоростью v = 10 м/с, и прилипает к его поверхности. Масса шарика m₂ = 10 г. Определите угловую скорость диска и линейную скорость точки В сразу после прилипания шарика(см. рис.).

24102
Сплошной медный диск массой 1 кг и толщиной 1 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов, перпендикулярно плоскости диска. Определить период такого физического маятника.

25183
Однородный диск радиуса R = 30 см совершает колебания вокруг горизонтальной оси, проходящей: а) через одну из образующих цилиндрической поверхности диска: б) середину одного из радиусов перпендикулярно плоскости диска. Какие периоды Т₁ и Т₂ его колебаний?