13550
Определите циркуляцию вектора магнитной индукции по окружности, через центр которой перпендикулярно ее плоскости проходит бесконечно длинный прямолинейный провод, по которому течет ток I = 5 А.

25925
Диск весом в 1 кг и диаметром 60 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с, какую работу надо совершить, чтобы остановить диск?

14631
Однородный диск радиусом R = 0,2 м и массой m = 0,5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости со вращения диска от времени t дается уравнением ω = А + Bt, где B = 8 рад/с². Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.

11087
По плоскости диска радиуса R = 10 см равномерно распределен заряд с поверхностной плотностью σ = 0,5 нКл/см². Диск равномерно вращается с частотой n = 1,8·10³ об/мин вокруг оси, проходящей через центр диска перпендикулярно его плоскости. Определить магнитный момент р_т, создаваемый вращающимся диском.

12090
Металлический диск радиусом 15 см, плоскость которого перпендикулярна однородному магнитному полю, вращается, совершая 10 оборотов в секунду. Ось вращения диска параллельна магнитному полю и проходит через его центр. Индукция магнитного поля 3 Тл. Определить разность потенциалов, которая возникает между центром и краем диска.

12454
Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу А надо совершить, чтобы остановить диск?

14539
Металлический диск радиуса R вращается с угловой скоростью ? вокруг оси, перпендикулярной диску и проходящей через его центр. Найти величину вектора напряженности электрического поля, возникшего на краю диска.

17681
Три проводника с токами I, I/4, 3I/4 лежат в одной плоскости и соединены в точке О. Найти напряженность магнитного поля на прямой, проходящей через точку О, перпендикулярной всем трем проводникам. (I = 10 А, расстояние до точки наблюдения 5 см).

20094
Найти массу азота, прошедшего вследствие диффузии через площадку 100 см² за 10 с, если градиент плотности в направлении, перпендикулярном площадке, равен 1,26 кг/м⁴. Температура азота 300 К, давление 0,1 МПа.

20163
Однородный диск массой m и радиусом R начинает вращаться вокруг неподвижной оси, проходящей через центр диска перпендикулярно его плоскости, под действием касательной силы, приложенной к ободу диска. Модуль силы зависит от времени как F = αt², где α — некоторая положительная постоянная. Найти угловую скорость ω₁ диска в момент времени t₁ после начала действия силы.

20169
Найти массу азота, прошедшего вследствие диффузии через площадку 0,01 м² за 10 с, если градиент плотности в направлении, перпендикулярном к площадке, 1,26 кг/м⁴. Температура азота 27°С, давление 10⁵ Па.

20406
Тонкий диск с постоянной плотностью заряда вращается вокруг оси, проходящей через центр перпендикулярно плоскости диска. Радиус диска а, заряд Q, угловая скорость вращения ω. Найдите индукцию магнитного поля в центре диска.

21021
Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Чему равны тангенциальные ускорения точки на краю диска в моменты времени t₁ = 2 с и t₂ = 7 с?

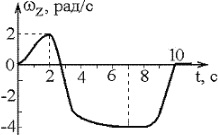
21346
Диск массой 50 кг и радиусом 25 см вращается вокруг неподвижной оси, проходящей перпендикулярно плоскости диска через его центр, делая 8,0 об/с. К ободу диска прижали тормозную колодку с силой 40 Н, под действием которой диск остановился через 10 с. Определить коэффициент трения.

21776
Диск радиусом 10 см с равномерно распределенным зарядом 1 мКл вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска, с частотой 10 оборотов в секунду. Определить магнитный момент диска.

25152
Тонкий диэлектрический диск радиуса R заряжен равномерно с поверхностной плотностью заряда σ. Определить напряженность электростатического поля в точке А, расположенной на оси х диска на расстоянии а от диска. Ось проходит через центр диска перпендикулярно его плоскости.

25153
Тонкий диск радиуса R заряжен равномерно по поверхности с плотностью заряда σ. Определить потенциал электростатического поля диска в точке А на оси x, проходящей через центр диска перпендикулярно его плоскости, на расстоянии a от центра.