11001
Определить линейную плотность заряда равномерно заряженного тонкого стержня длиной l = 10 см, если на продолжении оси на расстоянии a = 15 см от его середины напряженность электрического поля равна E = 1 кВ/м.

11724
Тонкий стержень длиной l = 10 см равномерно заряжен. Линейная плотность τ заряда равна 1 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

11665
Тонкий очень длинный стержень равномерно заряжен с линейной плотностью τ заряда, равной 10 мкКл/м. На перпендикуляре к оси стержня, восстановленном из конца его, находится точечный заряд Q = 10 нКл. Расстояние а заряда от конца стержня равно 20 см. Найти силу F взаимодействия заряженного стержня и точечного заряда.

11667
Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10 мкКл/м. Какова сила F, действующая на точечный заряд Q = 10 нКл, находящийся на расстоянии а = 20 см от стержня, вблизи его середины?

11672
Расстояние d между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью |τ| = 150 мкКл/м. Какова напряженность Е поля в точке, удаленной на r = 10 см как от первой, так и от второй проволоки?

14179
Тонкий стержень согнут в кольцо радиусом r = 5 см. Он равномерно заряжен с линейной плотностью τ = 800 нКл/см. Определить потенциал φ в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.

14323
На продолжении оси тонкого прямого стержня, равномерно заряженного с линейной плотностью заряда τ = 15 нКл/см на расстоянии а = 40 см от конца стержня находится точечный заряд q = 10 мкКл. Второй конец стержня уходит в бесконечность. Определить силу, действующую на заряд q.

14324
На продолжении оси тонкого прямого стержня, равномерно заряженного с линейной плотностью заряда τ = 400 нКл/см на расстоянии а = 30 см от конца стержня находится точечный заряд q = 20 мкКл. Второй конец стержня уходит в бесконечность. Определить силу, действующую на заряд q.

14759
По очень длинному тонкому стержню равномерно распределен электрический заряд с линейной плотностью τ = 0,5 мкКл/м. Определить в точке А, расположенной на перпендикуляре к стержню, напряженность E электрического поля (по модулю и направлению - угол β с осью Ох). Расстояние r₀ = 20 см.

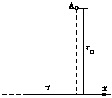
15952
Тонкий длинный стержень равномерно заряжен с линейной плотностью заряда 10 мкКл/м. На продолжении оси стержня на расстоянии 20 см от его конца находится точечный заряд q = 10^–8 Кл. Второй конец стержня уходит в бесконечность. Определить силу, с которой стержень действует на заряд.

16065
Тонкий бесконечно длинный стержень равномерно заряжен с линейной плотностью τ = 1,5 нКл/см. Определить силу, действующую на заряд Q = 0,2 мкКл, расположенный на расстоянии 10 см от стержня.

16068
Тонкий прямой стержень равномерно заряжен с линейной плотностью 3 мкKл/м. Вычислить напряженность электрического поля в точке, лежащей на оси стержня, на расстоянии 0,1 м от ближайшего конца.

16434
Тонкий стержень заряжен равномерно с линейной плотностью заряда 10³ нКл/м. Точечный заряд 50 нКл находится на продолжении оси стержня на расстоянии 10 см от ближайшего его конца. Стержень воздействует на заряд с силой 3 мН. Определить длину стержня.

16435
Тонкий стержень равномерно заряжен с линейной плотностью 2 нКл/см. На продолжении оси стержня на расстоянии 10 см от его конца находиться точечный заряд 0,2 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда.

16436
Тонкий стержень длиной l₀ = 10 см равномерно заряжен. Линейная плотность заряда τ = 17 мкКл/м. На продолжении стержня,на расстоянии l = 20 см от ближайшего его конца,находится точечный заряд q = 78 нКл. Найти силу F взаимодействия заряженного стержня и точечного заряда.

16437
Тонкий прямой стержень длиной l = 15 см равномерно заряжен с линейной плотностью τ = 0,10 мКл/м. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд q₀ = 10 нКл. Определить силу взаимодействия стержня и заряда.

16438
Тонкий стержень длины 20 см равномерно заряжен с линейной плотностью заряда 20 мКл/м. На продолжении оси стержня на расстоянии 10 см от его конца находится точечный заряд 10 мКл. Найдите силу взаимодействия заряженного стержня и точечного заряда.

16439
Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10^–7 Кл/м. На продолжении оси стержня на расстоянии а = 0,1 м от его конца находится точечный заряд 5·10^–9 Кл. Определить силу взаимодействия заряженного стержня и точечного заряда.

17280
Тонкий стержень длиной L = 20 см равномерно заряжен с линейной плотностью τ = 1,5·10^–7 Кл/м. На продолжении оси стержня на расстоянии 12 см находится заряд Q, на который действует сила F = 2,25·10^–3 Н. Чему равен заряд Q?

17302
Определить напряженность электрического поля, создаваемого стержнем длиной L = 6 см равномерно заряженным с линейной плотностью τ = 20·10^-6 Кл/м в точке, равноотстоящей от концов стержня на расстоянии S = 5 см.

17357
Стержень согнутый в полукольцо радиуса R = 5 см, заряжен линейной плотностью заряда τ = 133·10^–9 Кл/м. Какую работу надо совершить, чтобы перенести заряд Q = 6·10^–9 Кл из центра полукольца в бесконечность.

17364
Кольцо радиуса R = 10 см заряжен линейной плотностью τ = 3·10^–6 Кл/м. Какую работу надо совершить, чтобы перенести заряд Q = 10^–6 Кл из центра кольца в точку, расположенную на оси кольца на расстоянии L = 20 см от его центра.

17386
Два полубесконечных, тонких равномерно заряженных стержня расположены перпендикулярно друг к другу так, что точка пересечения их осей находится на расстоянии a = 8 см и b = 5 см от ближайших концов стержней. Найти силу, действующую на заряд q = 10 нКл, помещенный в точку пересечения осей стержней, полагая линейную плотность их зарядов одинаковой и равной τ = 1,5 нКл/см.

17391
Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R₁ = 5 cм и R₂ = 15см. Цилиндры заряжены равномерно разноименно с линейной плотностью 2,5·10^–9 Кл/м, причем заряд цилиндра меньшего радиуса отрицателен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком (ε = 3,0). Построить графики функций f₁(r) и f₂(r) для случаев: 1) r < R₁; 2) R₁ ≤ r ≤ R₂; 3) r > R₂. Вычислить разность потенциалов Δφ между точками r₁ = 2 см и r₂ = 14 см.

17392
Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R₁ = 6 cм и R₂ = 18 см. Цилиндры заряжены равномерно разноименно с линейной плотностью 5·10^–9 Кл/м, причем заряд цилиндра меньшего радиуса положителен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком (ε = 5,0). Построить графики функций f₁(r) и f₂(r) для случаев: 1) r < R₁; 2) R₁ ≤ r ≤ R₂; 3) r > R₂. Вычислить разность потенциалов Δφ между точками r₁ = 3 см и r₂ = 15 см.

17422
Тонкий стержень согнут в кольцо радиусом R = 10 см и заряжен с линейной плотностью τ = 300 нКл/м. Какую работу надо совершить, чтобы перенести заряд Q = 65 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии r = 20 см от его центра?

17423
Тонкий стержень согнут в кольцо радиуса R = 10 см и заряжен с линейной плотностью τ = 300 нКл/м. Какую работу А надо совершить, чтобы перенести заряд q = 50 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии l = 20 см его центра?

17424
Тонкий стержень согнут в кольцо радиуса R = 10 см. Он заряжен с линейной плотностью заряда τ = 300 нКл/м. Какую работу А надо совершить, чтобы перенести заряд q = 5 нКл из центра кольца в точку А, расположенную на оси кольца на расстоянии l = 20 см от его центра?

19894
Две длинные коаксиальные трубки радиусами R₁ = 2 см и R₂ = 4 см заряжены равномерно с линейной плотностью зарядов τ₁ = 1 нКл/м и τ₂ = –0,5 нКл/м соответственно. Пространство между трубками заполнено воздухом. Определить напряженность поля в точках, отстоящих от оси трубок на расстояниях 3 см и 5 см.

21068
Тонкий стержень равномерно заряжен с линейной плотностью τ = 10 нКл/м. Длина стержня равна L = 10 см. Определите напряженность электрического поля в точке, удаленной от концов стержня на расстояние, равное его длине.

23139
Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R₁ = 6 cм и R₂ = 18 см. Цилиндры заряжены равномерно и разноименно с линейной плотностью 5·10^–8 Кл/м, причем заряд цилиндра меньшего радиуса положителен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком (ε = 5,0). Построить графики функций E = f₁(r) и D = f₂(r) для случаев: 1) r < R₁; 2) R₁ ≤ r ≤ R₂; 3) r > R₂. Вычислить разность потенциалов Δφ между точками r₁ = 3 см и r₂ = 15 см.

23779
Определить напряжённость электростатического поля, создаваемого тонким длинным стержнем, равномерно заряженным с линейной плотностью заряда 20 мКл/м в точке, находящейся в 2 см от стержня.

24496
Тонкие стержни образуют квадрат со стороной длиной а = 0,1м. Стержни заряжены с линейной плотностью 30 нКл/м. Найти потенциал в центре квадрата.

10218
Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью заряда τ = 800 нКл/м. Определить потенциал φ в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.

10670
На продолжении оси тонкого прямого стержня, равномерно заряженного, с линейной плотностью заряда τ = 1 нКл/см на расстоянии а = 10 см от конца стержня находится точечный заряд Q = 0,1 мкКл. Второй конец стержня уходит в бесконечность. Определить силу взаимодействия стержня и точечного заряда, а также напряженность поля в точке, где находится заряд.

10680
С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно длинные параллельные нити с одинаковой линейной плотностью заряда t = 2 мкКл/м, находящиеся на расстоянии r = 4 см друг от друга?

10688
Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью t = 300 нКл/м. Определить потенциал в точке, расположенной на оси кольца на расстояние h = 20 см от его центра.