v0143
Дан перечень возможных значений ДСВ X: х₁ = –1, х₂ = 0, х₃ = 3, а также даны математические ожидания этой величины и ее квадрата: М(X) = 0,1, М(Х²) = 0,9. Найти вероятности р₁, р₂, р₃, которые отвечают возможным х₁, х₂, х₃.

Х	-1	0	3
р	р1	р2	р3

v0197
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
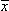
= 75,08; σ = 15; n = 225; γ = 0,95.

v0198
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
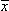
= 75,09; σ = 14; n = 196; γ = 0,95.

v0199
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
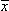
= 75,10; σ = 13; n = 169; γ = 0,95.

v0200
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
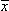
= 75,11; σ = 12; n = 144; γ = 0,95.

v0201
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
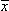
= 75,12; σ = 11; n = 121; γ = 0,95.

v0202
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
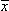
= 75,13; σ = 10; n = 100; γ = 0,95.

v0203
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
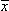
= 75,14; σ = 9; n = 81; γ = 0,95.

v0893
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
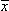
= 75,15; σ = 8; n = 64; γ = 0,95.

v0894
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
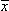
= 75,16; σ = 7; n = 49; γ = 0,95.

v0895
Найти доверительный интервал для оценки математического ожидания m нормального распределения с надёжностью 0,95, зная выборочную среднюю х, объём выборки n и среднее квадратическое отклонение.
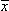
= 75,17; σ = 6; n = 36; γ = 0,95.

v1382
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 14; n = 25.

v1383
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 36; х_в = 15; n = 25.

v1384
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 49; х_в = 4; n = 50.

v1385
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 225; х_в = 11; n = 250.

v1386
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 4; х_в = 20; n = 200.

v1387
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 49; х_в = 17; n = 100.

v1388
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 16; х_в = 4; n = 40.

v1389
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 2500; х_в = 400; n = 65.

v1390
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 1; х_в = 1; n = 300.

v1391
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 81; х_в = 15; n = 30.

v1392
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 144; х_в = 1; n = 25.

v1393
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 16; х_в = 5; n = 100.

v1394
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 9; х_в = 16; n = 45.

v1395
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 64; х_в = 10; n = 250.

v1396
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 0,25; х_в = 1,4; n = 35.

v1397
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 140; n = 250.

v1398
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 16; х_в = 4; n = 60.

v1399
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 14; n = 100.

v1400
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 4; х_в = 3; n = 100.

v1401
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 10; n = 25.

v1402
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 14; n = 65.

v1404
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 40; n = 35.

v1405
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 225; х_в = 140; n = 250.

v1406
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 1; х_в = 1; n = 500.

v1407
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 81; х_в = 14; n = 55.

v1408
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 1; n = 25.

v1409
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 25; х_в = 1; n = 50.

v1410
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 36; х_в = 12; n = 100.

v1411
Найти доверительный интервал с надежностью 0,95 для оценки неизвестного математического ожидания а нормально распределенной случайной величины ξ, если известна дисперсия σ², выборочное среднее х_в и объем выборки n. σ² = 49; х_в = 10; n = 100.

v1605
Был измерен рост 50 произвольно взятых студентов. Получены следующие данные: 147, 154, 156, 157, 159, 160, 187, 164, 183, 176, 172, 174, 161, 177, 163, 173, 171, 174, 161, 184, 160, 177, 161, 171, 179, 162, 178, 164, 172, 163, 174, 172, 171, 168, 172, 174, 164, 168, 172, 163, 166, 174, 173, 162, 167, 162, 161, 172, 167, 171. Длина интервала равна 5 см. Составить интервальный ряд распределения с заданной длиной интервала. Для полученного ряда найти: 1) выборочное среднее; 2) среднее квадратичное; 3) построить доверительные интервалы для математического ожидания и дисперсии.