10559
Стационарный искусственный спутник движется по окружности в плоскости земного экватора, оставаясь все время над одним и тем же пунктом земной поверхности. Определить угловую скорость ω спутника и радиус r его орбиты.

13030
Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением а_τ. К концу четвертого оборота после начала движения линейная скорость точки v₁ = 15 см/с Определите нормальное ускорение а_n2 точки через t₂ = 16 с после начала движения.

13089
Материальная точка массой m = 20 г движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением. К концу пятого оборота после начала движения кинетическая энергия материальной точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение.

15996
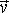
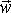
За промежуток времени τ = 10,0 с точка прошла половину окружности радиуса R = 160 см. Вычислить за это время: а) среднюю скорость (v); б) модуль среднего вектора скорости |<>|; в) модуль среднего вектора полного ускорения |<>|, если точка двигалась с постоянным тангенциальным ускорением.

40485
Точка движется по окружности радиусом R = 4 м так, что в каждый момент времени ее нормальное и тангенциальное ускорения равны по модулю. В начальный момент времени t = 0 скорость точки V₀ = 0,2 м/с. Найти скорость точки в момент времени t₁ = 10 c.

40541
Точка движется по окружности радиусом 8 м с постоянным тангенциальным ускорением, равным 57 см/с². Через сколько времени после начала движения нормальное ускорение точки будет вдвое больше тангенциального?

40565
Точка движется по окружности с постоянным угловым ускорением ε = 3,00 рад/с. Определить радиус окружности, если к концу первой секунды после начала движения полное ускорение точки а = 7,50 м/с.

40584
Точка движется по окружности радиусом 0,4 м согласно уравнению S = 2-cos2t. Определить нормальное ускорение точки в момент времени t = π/4 с?

14457
Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением s = Ct³, где С = 0,1 см/с³. Найти нормальное a_n и тангенциальное a_τ ускорения точки в момент, когда линейная скорость точки v = 0,3 м/с.

11009
По окружности радиусом R = 5 м равномерно движется материальная точка со скоростью v = 5 м/с. Построить графики зависимости длины пути s и модуля перемещения |Δr| от времени t. В момент времени, принятый за начальный (t = 0), s(0) и |Δr(0)| считать равными нулю.

11210
Точка движется по окружности радиусом 60 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 5 м/с.

12253
Материальная точка массой 2·10^–3 кг движется по окружности радиусом 2м. Её угловая скорость зависит от времени согласно уравнению ω = 0,4t² c^–1. Определить для момента времени 2с: силу, действующую по касательной к траектории; нормальное, касательное и полное ускорение точки; кинетическую энергию.

15007
Точка движется по окружности радиусом R = 1,20 м. Уравнение движения точки имеет вид: φ = At + Bt³, где А = 0,500 рад/с, В = 2,50 рад/с³. Определить тангенциальное а_τ, нормальное а_п и полное а ускорение точки в момент времени t = 0,954 с.

15131
Определить скорость и полное ускорение точки в момент времени 2 с, если она движется по окружности радиусом 1 м согласно уравнению φ = At + Bt³, где А = 8 м/с, В = –1 м/с³, t — криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности. Изобразить векторы скоростей и ускорений (линейных и угловых) для случая, когда окружность расположена в горизонтальной плоскости в указанный момент времени.

15623
Материальная точка движется по окружности радиуса 80 см по закону S = 10t–0,1t³ (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.

19827
Материальная точка движется по окружности радиусом R = 4 м. Закон ее движения описывается уравнением ξ = A+Bt², где A = 8 м, B = –2 м/с², а ξ отсчитывается вдоль окружности. Найти момент времени, когда нормальное ускорение точки равно 9 м/с², а также скорость, тангенциальное и полное ускорения точки в этот момент времени.

19831
Материальная точка движется по окружности радиуса R = 2 м. Закон ее движения описывается уравнением ξ(t) = At² + Bt³, где А = 3 м/с², В = 1 м/с³, а координата ξ(t) отсчитывается вдоль окружности. Найти момент времени, когда тангенциальное ускорение точки равно 18 м/с², а также нормальное и полное линейное ускорение точки в этот момент времени.

21514
Материальная точка массой 1 г движется по окружности радиусом 1 м согласно уравнению S = 8t – 0,2t³. Определите скорость, тангенциальное ускорение, нормальное ускорение в момент времени t = 2 с.

22187
Точка движется по окружности радиусом 79 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 3 м/с.

22203
Точка движется по окружности радиусом R = 0,1 м с постоянным тангенциальным ускорением. Найти ускорение точки через 10 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 0,8 м/с.

22627
Человек массой 60 кг находится на неподвижной платформе массой 100 кг. Какова будет частота вращения платформы, если человек будет двигаться по окружности радиусом 5 м вокруг оси вращения со скоростью 4 км/ч относительно Земли? Диаметр платформы - 10 м. Считать платформу однородным диском, а человека - материальной точкой.

24007
Точка движется по окружности радиусом 1 м с постоянным тангенциальным ускорением, равным 73 см/с². Через сколько времени после начала движения нормальное ускорение точки вдвое больше тангенциального?

24033
Материальная точка движется по окружности, радиус которой 40 м. Зависимость пути, пройденного точкой, от времени задана уравнением s = 2t³ + 4t² – 2t + 10. Определить пройденный путь, угловую скорость и угловое ускорение точки через 5 с от начала ее движения.

24400
Человек массой m₁ = 70 кг находится на неподвижной платформе массой m₂ = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиусом r = 5 м вокруг оси вращения? Скорость движения человека относительно платформы v = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека – материальной точкой.

24546
Точка движется по окружности радиусом 20 см с постоянным касательным ускорением 0,5 м/с². Через сколько времени после начала движения нормальное ускорение точки будет равно тангенциальному ускорению?

24583
Материальная точка движется по окружности, радиус которой равен 2 м. Уравнение движения имеет вид ξ(t) = At + Bt³, где А = 0,5 м/с, B = 0,1 м/с³, а ξ — криволинейная координата, отсчитываемая вдоль окружности. Найти угловые скорость и ускорение, а также линейное ускорение материальной точки в момент времени t = 2 с.