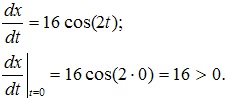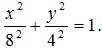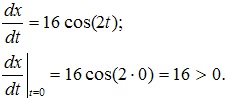Точка участвует одновременно в двух
Пример решения задачи 10072
Условие Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A
1sinω
1t и у=А
2cosω
2t, где A
1=8 см, A
2=4 см, ω
1=ω
2=2 с
–1. Написать уравнение траектории и построить ее. Показать направление движения точки.
Краткое условие
х=A
1sin(ω
1t) у=A
2sin(ω
2t)
А
1=8 см
А
2=4 см
ω
1=ω
2=2 с
–1
Найти
f(x,y) ― ?
Решение
Преобразуем уравнения колебаний в уравнение кривой второго порядка и выясним форму кривой. Кривые второго порядка бывают трех типов: эллипс, гипербола, парабола. А также бывают вырожденные случаи ― две пересекающиеся прямые или одна прямая или точка. Эллипс может быть вырожден в окружность.
x=8sin(2t);
x
2=64sin2(2t);
x
2/4=16sin2(2t). (1)
y=4cos(2t);
y
2=16cos2(2t). (2)
Прибавим почленно уравнения (1) и (2):
х
2/4+у
2=16;
х
2/64+у
2/16=1;
х
2/8
2+у
2/4
2=1 ― уравнение траектории ― уравнение эллипса с полуосями 8 и 4.
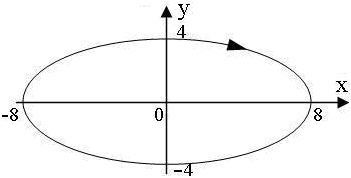
Чтобы определить направление движения точки, выберем точку траектории, например, (0; 4), и найдем знак производной dx/dt. Это будет направление скорости: плюс ― вправо, минус ― влево.
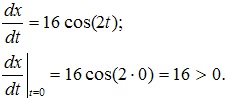
В точке (0; 4) направление движения вправо. Изображаем это на рисунке стрелкой.
Ответ: 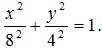
40666
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = sinπt, y = 4sin(πt + π). Найти траекторию движения точки, построить ее с соблюдением масштаба.
40699
Точка участвует в двух колебаниях одного направления х1 = A1Cosωt і х2 = A2Cos(ω(t+τ)), де А1 = 4 см, А2 = 3 см, ω = π рад/с, τ = 0,5 с. Выполнить рисунок и методом векторных диаграмм найти уравнение результирующих колебаний.
70314
На кольцевой трассе длиной 4 км стартуют одновременно два автомобиля. Время прохождения одного круга первым автомобилем = 2 минуты, а вторым – 2 мин 03 секунды. После 20-го круга у первого автомобиля произошла поломка и его скорость уменьшилась на 10 км/ч. Успеет ли второй автомобиль обогнать первый и прийти к финишу раньше, если каждый автомобиль должен проехать 36 кругов.
12655
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых в единицах СИ имеют вид x = 0,4 cos πt и у = 0,2 cos π(t–0,5). Определить траекторию движения точки и начертить ее с соблюдением масштаба. Рассчитать и указать на чертеже скорость и ускорение точки в начальный момент времени и указать направление ее движения по кривой. Если траектория не замкнутая, то указать пределы движения.
20381
Материальная точка участвует одновременно в двух колебаниях одного направления x1 = 5 sin (2t + π/4), см и х2 = 15 sin 2t, см. Записать уравнение результирующего колебания. Определить скорость точки через 0,2 с.
20382
Складываются два колебания одного направления, происходящие по закону косинуса, с одинаковыми амплитудами 0,1 м и одинаковыми начальными фазами, частоты которых равны 50 и 50,6 Гц. Записать уравнение результирующего колебания.
21756
Написать уравнение движения x(t) частицы, одновременно участвующей в двух колебаниях одного направления: x1 = 30cos πt/3 и x2 = 30cos(πt/3 + π/6) (мм).
22635
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x1 = 0,1cos πt/2 и x2 = 0,12cos π(t+1)/2. Определить уравнение результирующих колебаний.
22910
Точка участвует одновременно в двух гармонических колебаниях одного направления: X1 = 3 Cos 10,4πt, см; Х2 = 3 Cos 10πt, см. Записать уравнение результирующего колебания. Определить период биения, период колебания и число колебаний точки за один период биения. Укажите значение max и min амплитуды результирующего колебания.
23133
Материальная точка участвует в двух колебаниях, выраженных уравнениями х1 = 3 cos t, см, х2 = 3 cos (t + π/3), см. Написать уравнение результирующего колебания.
23613
Материальная точка участвует в двух колебаниях одинакового периода с начальными формами π/6 и π/3. Амплитуды колебаний 4 см и 6 см. Найти амплитуду результирующего колебания, если колебание произойдет в одном направлении.
10576
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых: x = A1 sin ω1t и y = A2 cos ω2t, где A1 = 2 см; A2 = 1 см; ω1 = ω2 = 1 с–1. Написать уравнение траектории и построить ее на чертеже; показать направление движения точки.
25168
Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых в единицах СИ имеют вид x = 0,3 cos(π∙t) и y = 0,4 sin (π∙t). Найти уравнение траектории движения точки, начертить ее с соблюдением масштаба и указать направление движения точки по кривой.