10574
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x = A₁cos ω₁t и y = A₂sin ω₂t, где А₁ = 1 см; ω₁ = 0,5 с^–1; A₂ = 1 см; ω₂ = 1 с^–1. Найти уравнение траектории построить ее с соблюдением масштаба и указать направление движения.

11308
Точка совершает гармонические колебания. Наибольшее смещение x_max точки равно 10 см, наибольшая скорость 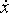_max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение 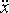_max точки.

11321
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A₁cosωt и y = A₂cosω(t+τ), где А₁ = 4 см, A₁ = 8 см, ω = π c^–1, τ = 1 с. Найти уравнение траектории точки и построить график ее движения.

11322
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями: 1) x = Acosωt и y = Acosωt; 2) x = Acosωt и y = A₁cosωt; 3) x = Acosωt и y = Acos(ωt+φ₁); 4) x = A₂cosωt и y = Acos(ωt+φ₂); 5) x = A₁cosωt и y = A₁sinωt; 6) x = Acosωt и y = A₁sinωt; 7) x = A₂sinωt и y = A₁sinωt; 8) x = A₂sinωt и y = Asin(ωt+φ₂). Найти (для восьми случаев) уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26197
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = Acosωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26198
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = A₁cosωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26199
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = Acos(ωt+φ₁). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26200
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A₂cosωt и y = Acos(ωt+φ₂). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26201
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A₁cosωt и y = A₂sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26202
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = Acosωt и y = A₁sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26203
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A₂sinωt и y = A₁sinωt. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

26204
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями x = A₂sinωt и y = Asin(ωt+φ₂). Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А = 2 см, A₁ = 3 см, А₂ = 1 см; φ₁ = π/2, φ₂ = π.

11324
Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A₁sinωt и y = A₂cosωt, где А₁ = 0,5 см; A₂ = 2 см. Найти уравнение траектории точки и построить ее, указав направление движения.

11377
Точка совершает одновременно два колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 8cosπt, y = 8cosπ(t+1) (длина в сантиметрах, время в секундах). Найти уравнение траектории и построить график её движения.

15101
Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,60 с и амплитудой а = 10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь а/2: а) из крайнего положения; б) из положения равновесия.

19950
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 4cosπt см и y = 8cos(πt+π) см. Найдите уравнение траектории точки и постройте график ее движения.

21121
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Уравнения колебаний х = A cos ωt и у = A cos (ωt + φ). Определить уравнение траектории точки в виде f(x, у) = 0. Принять А = 2 см, φ = π/2.

21409
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями х = 4 cos πt см и у = 2 sin π(t + 1) см. Найти уравнение траектории точки и построить график ее движения.

22014
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x₁ = 0,1cos π(t+1/6) и x₂ = 0,05cos π(t+1/2). Определить уравнение результирующих колебаний.

22015
Материальная точка участвует одновременно в двух гармонических колебаниях, проходящих вдоль одной прямой. В единицах СИ уравнения слагаемых колебаний записываются в виде x₁ = 0,1cos πt/2 и x₂ = 0,12 cos π(t+1)/2. Определить уравнение результирующих колебаний.

23457
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями х = А₁cos ωt и у = А₂cos ω(t + τ), где А₁ = 4 см, А₂ = 8 см, ω = π с^–1, τ = 1 с. Найти уравнение траектории точки и построить ее с соблюдением масштаба, указав направление движения точки. Поясните свой ответ.

23471
Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: x = 2cosωt см и y = cosωt см. Запишите уравнение траектории результирующего движения точки и постройте ее с соблюдением масштаба.