10202
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = 4σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 30 нКл/м², r = 1,5R; 3) построить график E(r).

60611
Поле создается сплошным стеклянным бесконечно протяженным цилиндром радиуса R = 15 см. Объемная плотность его равна 20 нКл/м³. Определить напряженность поля как функцию расстояния от центра цилиндра, используя теорему Гаусса. Построить график зависимости E = f(r). ε = 7.

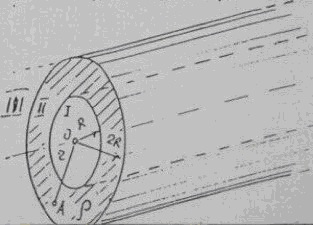
15908
В бесконечном цилиндре радиуса 2R, несущим равномерно распределенный заряд с объемной плотностью ρ = 6 мкКл/м³, сделан соосный, цилиндрический вырез радиусом R.
1. Используя теорему Остроградского-Гаусса, найти выражение для напряженности Е(r) электрического поля в трех областях (I, II, III).
2. Вычислить напряженность Е, поля в точке А, удаленной от оси цилиндра на расстояние τ = 1,5R, и указать направление вектора Е_A.
3. Построить график Е(r) в единицах ρR/ε₀. R = 2 см.

17560
Используя теорему Гаусса, найдите напряженность поля, создаваемого сплошным эбонитовым шаром радиуса R = 10 см, как функцию расстояния r от центра шара. Объемная плотность заряда шара равна ρ = 10 нКл/м³. Постройте график зависимости Е = f(r). Диэлектрическая проницаемость эбонита ε = 2,6.