Газ получил от нагревателя количество теплоты

50443
Двухатомный газ в количестве ν = 2 моль совершает цикл Карно. При изотермическом расширении газа его объем увеличивается в β = 2 раза, а при последующем адиабатическом расширении он совершает работу А₂₃ = 300 Дж. Наибольшее давление газа равно р₁ = 1,2 МПа, а температура «нагревателя» составляет t_н = 150°С. Определите: 1) параметры состояния воздуха (р_k, V_k и T_k, где k = 1, 2, 3, 4) в характерных точках цикла; 2) работу газа A за один цикл; 3) количество теплоты Q_н, полученное рабочим телом от «нагревателя» за цикл; 4) термический КПД цикла.

11635
Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты Q₁, полученного от нагревателя, отдает охладителю. Температура Т₂ охладителя равна 280 К. Определить температуру T₁ нагревателя.

11431
В идеальном тепловом двигателе температура нагревателя в 3 раза выше температуры охладителя. Количество теплоты получил газ от нагревателя, если выполненная им полезная работа составляет А = 10 кДж?

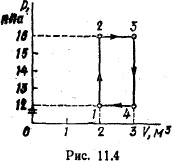
11624
Идеальный двухатомный газ, содержащий количество вещества ν = 1 кмоль, совершает замкнутый цикл, график которого изображен на рис. 11.4. Определить: 1) количество теплоты Q₁, полученное от нагревателя; 2) количество теплоты Q₂, переданное охладителю; 3) работу А, совершаемую газом за цикл; 4) термический КПД η цикла.

11625
Одноатомный газ, содержащий количество вещества ν = 0,1 кмоль, под давлением p₁ = 100 кПа занимал объем V₁ = 5 м³. Газ сжимался изобарно до объема V₂ = 1 м³, затем сжимался адиабатно и расширялся при постоянной температуре до начальных объема и давления. Построить график процесса. Найти: 1) температуры T₁, T₂, объемы V₁, V₂ и давление p₃, соответствующее характерным точкам цикла; 2) количество теплоты Q₁, полученное газом от нагревателя; 3) количество теплоты Q₂, переданное газом охладителю; 4) работу А, совершенную газом за весь цикл; 5) термический КПД η цикла.

11631
Идеальный газ совершает цикл Карно. Температура T₁ нагревателя в четыре раза выше температуры Т₂ охладителя. Какую долю w количества теплоты, получаемого за один цикл от нагревателя, газ отдает охладителю?

11633
Идеальный газ, совершающий цикл Карно, получив от нагревателя количество теплоты Q₁ = 4,2 кДж, совершил работу А = 590 Дж. Найти термический КПД η этого цикла. Во сколько раз температура T₁ нагревателя больше температуры Т₂ охладителя?

13880
Газ, осуществляющий цикл Карно, за счет каждого килоджоуля теплоты, полученной от нагревателя, выполняет работу 140 Дж. Во сколько раз абсолютная температура нагревателя выше абсолютной температуры холодильника?

14077
Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке.

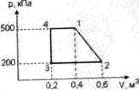
1) Найдите работу газа в этом циклическом процессе.
2) Чему равно количество теплоты, полученное при этом процессе?
3) Чему равен КПД этого цикла?

15109
Баллон с углекислым газом объемом 80 литров при давлении p₁ = 9,3 МПа доставляют со склада, где температура t₁ = –8 °C, в помещение с температурой t₂ = 24 °C. Определить каким станет давление газа в баллоне, и какое количество теплоты он получит?

16211
Газ, расширяясь, переходит из одного и того же начального состояния с объемом V₁ в конечное состояние с объемом V₂: а) адиабатически; б) изобарически. В каком процессе газ получает наибольшее количество тепла, а в каком совершает наибольшую работу? Нарисуйте графики процессов в координатах P-V. Ответ обоснуйте.

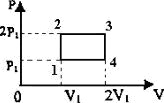
16469
Азот совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Суммарное количество теплоты, полученное газом Q в этом круговом процессе, равно 1) 4P₁V₁; 2) 6,5P₁V₁; 3) 9,5P₁V₁; 4) 12P₁V₁.

16481
10 г кислорода находится под давлением 3·10⁵ Па при температуре 10°С. После нагревания при постоянном давлении газ занял объем 10 л. Найти: 1) количество тепла, полученного газом; 2) энергию теплового движения молекул газа до и после нагревания.

17458
Газ, расширяясь, переходит из одного и того же начального состояния с объемом V₁ в конечное состояние с объемом V₂: а) изотермически: б) адиабатически. В каком процессе газ получает наименьшее количество теплоты и совершает наибольшую работу? Постройте график процессов в координатах P-V.

17493
Некоторый газ массой m = 0,1 кг при определенных условиях имеет коэффициент вязкости η = 8,6·10^–6 Па·с и коэффициент теплопроводности λ = 89,9·10^–3 мВт/(м·К). На сколько увеличится температура газа, если при изохорном нагревании он получит количество теплоты Q = 20 Дж?

17885
Идеальный газ совершает цикл Карно. Температура нагревателя в три раза выше температуры холодильника. Какую долю количества теплоты, получаемого за один цикл от нагревателя, газ отдает холодильнику?

11629
Совершая замкнутый процесс, газ получил от нагревателя количество теплоты Q₁ = 4 кДж. Определить работу А газа при протекании цикла, если его термический КПД η = 0,1.

20012
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот
Т₁ = 420 К
Р₁ = 2,1·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20013
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — аргон
Т₁ = 420 К
Р₁ = 2·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20014
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — аргон
Т₁ = 420 К
Р₁ = 2·10⁵ Па
V₁ = 1 л = 1·10^–3 м³
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20015
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — водород
Т₁ = 400 К
Р₁ = 1,9·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20016
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — водород
Т₁ = 400 К
Р₁ = 1,9·10⁵ Па
V₁ = 1 л = 1·10^–3 м³
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20017
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — кислород
Т₁ = 400 К
Р₁ = 1,8·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20018
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — гелий
Т₁ = 450 К
Р₁ = 1,7·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20019
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот гелий
Т₁ = 450 К
Р₁ = 1,7·10⁵ Па
V₁ = 1 л = 1·10^–3 м³
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20020
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — воздух
Т₁ = 450 К
Р₁ = 1,6·10⁵ Па
V₁ = 2 л = 2·10^–3 м³
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

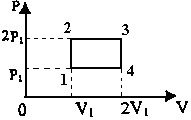
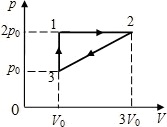
20653
Кислород совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Отношение работы A₂₃, совершенной газом на участке 2–3, к количеству теплоты Q₁₂, полученного газом на участке 1–2, A₂₃/Q₁₂ равно ... 1) 0,5; 2) 1; 3) 1,33; 4) 2,5.

20656
При переходе из состояния 1 в состояние 4 отношение количества теплоты Q₁₄, полученного двухатомным газом к работе A₁₄, совершенной газом в этом процессе, Q₁₄/A₁₄ равно ... .

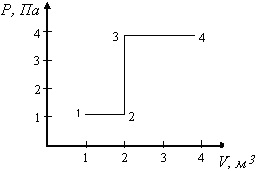
20699
На графике изображен цикл с идеальным одноатомным газом неизменной массы количеством ν = 2 моль. Представьте график цикла в координатах Р–V и Определите количество теплоты, полученное газом за цикл, если параметры газа в состоянии 1 равны Т₁ = 300 К, а давление Р₁ = 10⁵ Па.

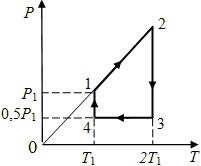
20700
Два моля идеального одноатомного газа сначала изобарно нагрели, а затем, изохорно охладили до первоначальной температуры, при этом давление газа уменьшилось в три раза (см. рис.). После этого система изотермически вернулась в начальное состояние. Начальная температура газа равна Т = 400 К. Какое количество теплоты получил газ за весь процесс?

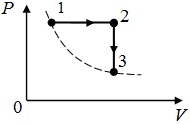
20708
С одноатомным идеальным газом неизменной массы в количестве ν = 1 моль происходит циклический процесс, показанный на рисунке. За цикл газ совершает работу А = 5 кДж. Какое количество теплоты получает газ за цикл? Чему равен КПД цикла?

21372
Какое количество углекислого газа продиффундирует из почвы в атмосферу за 1 час с поверхности грядки шириной 50 см и длиной 18 м, если видимая поверхность грядки в 1,5 раз меньше поверхности почвы, полученной при ее рыхлении? Коэффициент диффузии газов принять в среднем 0,05 см²/с, а градиент плотности газа 4·10^–5 г/см⁴.

24826
Кислород массой m = 0,5 кг (M = 0,032 кг/моль) при температуре Т = 320 К охладили изохорно, вследствие чего его давление уменьшилось в n = 3 раза. Затем газ изобарно расширили так, что температура его стала равной первоначальной. Найдите работу газа. Как изменилась его внутренняя энергия? Какое количество теплоты получил газ?