40551
Найти полное ускорение в момент времени t = 3 c точки, находящейся на ободе колеса радиусом R = 0,5 м, вращающегося согласно уравнению φ = Аt + Вt³, где А = 2 рад/с, В = 0,2 рад/с³.

40606
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Вt² (А = 0,3 м/с², В = 0,1 м/с³). Определить момент времени, для которого вектор полного ускорения a образует с радиусом колеса угол φ = 45°.

14446
Найти радиус R вращающегося колеса, если известно, что линейная скорость v₁ точки, лежащей на ободе, в 2,5 раза больше линейной скорости v₂ точки, лежащей на расстоянии r = 5 см ближе к оси колеса.

14462
Колесо радиусом R = 5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = А + Bt + Ct² +Dt³, где D = 1 рад/с³. Для точек, лежащих на ободе колеса, найти изменение тангенциального ускорения Δa_τ за единицу времени.

14463
Колесо радиусом R = 5 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени дается уравнением v = At + Bt², где А = 3 см/с² и В = 1 см/с³. Найти угол α, составляемый вектором полного ускорения с радиусом колеса в моменты времени t, равные: 0, 1, 2, 3,4 и 5 с после начала движения.

14464
Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = А + Bt + Ct² + Dt³, где В = 1 рад/с, С = 1 рад/с² и D = 1 рад/с³. Найти радиус R колеса, если известно, что к концу второй секунды движения для точек, лежащих на ободе колеса, нормальное ускорение а_n = 3,46·10² м/с².

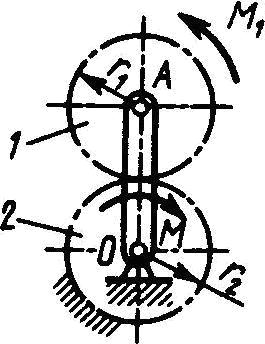
26621
К зубчатому колесу 1 приложена пара сил с моментом М₁ = 40 Н·м. Определить момент М пары сил, который необходимо приложить к кривошипу ОА, для того чтобы механизм находился в равновесии, если радиусы r₁ = r₂.

12870
Уравнение вращения колеса радиусом R = 0,5 м имеет вид φ = At + Bt⁵, где А = 2 рад/с; В = 0,5 рад/с⁵. Определить полное ускорение в момент t = 1 с точки, находящейся на ободе колеса.

13322
Диск радиусом R = 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A + Bt³ (А = 2 рад, B = 4 рад/с³). Определите для точек на ободе колеса 1) нормальное ускорение а_п в момент времени t = 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота φ, при котором полное ускорение составляет с радиусом колеса угол α = 45°.

24797
Колесо вращается по закону φ = 4 + 5t – t³. Найти линейную скорость в конце второй секунды, полное ускорение точек находящегося на ободе колеса радиусом 2 см.