10958
Микрочастица массой 10^–30 кг находится в одномерной потенциальной яме с вертикальными стенками. Найти отношение разности энергий пятого и четвёртого энергетических уровней к энергии частицы в состоянии с квантовым числом n = 4.

11216
Электрон находится в одномерной потенциальной яме с вертикальными стенками. Найти отношение разности энергий электрона на втором и третьем энергетических уровнях к подобной разности энергий для микрочастицы массой 2·10^–26 кг.

11217
Микрочастица находится в одномерной потенциальной яме шириной а на четвертом энергетическом уровне. Определить отношение плотностей вероятности обнаружения частицы в середине ямы и на расстоянии а/5 от края ямы.

11218
Частица массой 6,68·10^–27 кг находится в третьем возбужденном состоянии в одномерной прямоугольной потенциальной яме. Максимальное значение плотности вероятности координаты частицы равно 1,7·10¹⁰ м^–1. Найти в эВ энергию частицы в данном состоянии.

11238
Используя соотношение неопределенностей, оценить в эВ минимальную энергию микрочастицы (m = 6,68·10^–27 кг), находящейся в одномерной потенциальной яме шириной а = 3,29 нм.

12108
Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале L/4 равноудаленном от стенок одномерной потенциальной ямы шириной L.

13747
Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в основном состоянии. Определите вероятность обнаружения частицы во второй четверти.

14140
Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Какова вероятность обнаружения электрона в средней трети ямы, если электрон находится во втором возбуждённом состоянии? Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

14194
Электрон находится в бесконечно глубокой одномерной потенциальной яме. Во сколько раз различаются вероятности обнаружения электрона в средней части ямы на отрезке Δx = l/4, равноудаленном от стенок ямы: 1) в его основном энергетическом состоянии; 2) в возбужденном состоянии с n = 2.

14276
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 490,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, х₂) обнаружения частицы в интервале от x₁ = 0 до х₂ = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14369
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 37,68эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,1l до х₂ = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14370
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 37,68 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, х₂) обнаружения частицы в интервале от x₁ = 0 до х₂ = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14383
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 601,7 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, х₂) обнаружения частицы в интервале от x₁ = 0 до х₂ = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14384
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 601,7 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,1l до х₂ = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14526
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 1354 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0 до х₂ = 0,1l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

14527
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 1354 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,1l до х₂ = 0,2l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16268
Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n = 2). Определите вероятность обнаружения частицы в области (3/8)l < x < (5/8)l.

16405
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 338,5 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,1l до х₂ = 0,2l. Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16542
Частица электрон с энергией E_n = 1354 эВ находится в одномерной прямоугольной бесконечной потенциальной яме шириной l. Найти главное квантовое число n и вычислить вероятность обнаружения частицы Р(х) в интервале от 0,7l до 0,8l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность. Масса электрона m_е = 9,1·10^–31 кг, ширина потенциальной ямы l = 10^–10 м.

16603
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 338,5 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность р(х₁, х₂) обнаружения частицы в интервале от х₁ = 0 до х₂ = 0,1l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16606
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0 до х₂ = 0,4l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16607
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,1l до х₂ = 0,2l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16608
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 150,4 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,2l до х₂ = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16609
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 940,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от x₁ = 0,1l до x₂ = 0,2l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16617
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 940,2 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, х₂) обнаружения частицы в интервале от x₁ = 0 до х₂ = 0,1l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16619
Частица электрон с энергией E_n = 601,7 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0 до х₂ = 0,2l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16620
Частица электрон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Энергия частицы W_n = 338,5 эВ. 1) Найти квантовое число n, характеризующее энергетическое состояние частицы. 2) Вычислить вероятность P(х₁, х₂) обнаружения частицы в интервале от х₁ = 0,2l до х₂ = 0,3l. 3) Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

16621
Частица электрон с энергией E_n = 338,4 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,5l до х₂ = 0,6l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16625
Частица электрон с энергией E_n = 940,2 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,2l до х₂ = 0,5l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16627
Частица электрон с энергией E_n = 150,4 эВ находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–10 м. Найти главное квантовое число n и вычислить вероятность обнаружения частицы P(x) в интервале от х₁ = 0,1l до х₂ = 0,3l. Построить график зависимости волновой функции Ψ_n(x) и плотности вероятности |Ψ_n(x)|² обнаружения частицы в потенциальной яме от координаты x. Указать на графике найденную вероятность.

16695
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 8,191 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(х₁,х₂) обнаружения частицы в интервале от х₁ = 0,3l до х₂ = 0,4l. Построить зависимость от координаты х плотности вероятности |Ψ_n(х)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

17244
Электрон в одномерной прямоугольной потенциальной яме шириной l = 1 нм с бесконечно высокими стенками находится в возбуждённом состоянии с n = 4. Определить: 1) энергию электрона; 2) вероятность обнаружения электрона в первой четверти ямы. Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения частицы в данном состоянии.

18065
В одномерной прямоугольной потенциальной яме шириной 0,3 нм с бесконечно высокими стенками в третьем возбужденном состоянии находится электрон. Определить: 1) минимальную энергию электрона; 2) вероятность обнаружения электрона в средней трети ямы.

16604
Частица протон находится в одномерной прямоугольной бесконечно глубокой потенциальной яме шириной l = 10^–11 м. Энергия частицы W_n = 18,43 эВ. Найти квантовое число n, характеризующее энергетическое состояние частицы. Вычислить вероятность Р(x₁, х₂) обнаружения частицы в интервале от x₁ = 0,4l до x₂ = 0,5l. Построить график зависимости от координаты х плотности вероятности |Ψ_n(x)|² обнаружения частицы. Показать на построенной зависимости найденную вероятность.

21305
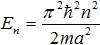
Микрочастица с массой m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками шириной а. Разрешенные значения энергии микрочастицы определяются формулой , где n = 1,2,3... Находясь в основном состоянии, микрочастица поглотила фотон с энергией Е = 45 эВ и перешла на четвертый энергетический уровень. Найти наименьший импульс фотона, который может быть излучен этой частицей.
а) 3,1·10–26 кг·м/с; б) 2,5·10–26 кг·м/с; в) 2,1·10–26 кг·м/с;
г) 1,5·10–26 кг·м/с; д) 1,1·10–26 кг·м/с.

21375
Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Какова вероятность обнаружения электрона в средней трети ямы, если электрон находится в первом возбуждённом состоянии (n = 2)? Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

21377
Электрон находится в одномерной прямоугольной ''потенциальной яме" шириной l с бесконечно высокими "стенками". Определите вероятность W обнаружения электрона в средней трети "ямы", если электрон находится в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

21984
Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найдите ширину ямы, если минимальное энергетическое расстояние между уровнями электрона в яме равно тепловой энергии KT при комнатной температуре.

22489
Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Найдите вероятность обнаружить частицу в области l/3 < х < 2l/3. Сравните её с вероятностью обнаружить классическую частицу в этой же области.