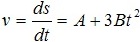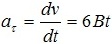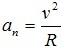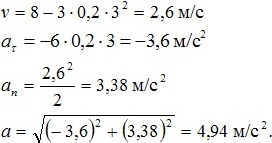тангенциальное нормальное полное ускорения
Пример решения задачи 10503
Условие Материальная точка движется по окружности радиуса R = 2 м согласно уравнению S = At+Bt
3, где А = 8 м/с; В = –0,2 м/с
3. Найти скорость v, тангенциальное a
t, нормальное a
n и полное а ускорения в момент времени t = 3 с.
Краткое условие
R = 2 м
s = At + Bt
3
А = 8 м/с
В = −0,2 м/с
3
t = 3 с
Найти
v ― ?
a
τ ― ?
a
n ― ?
a ― ?
Решение
Скорость точки изменяется по закону
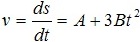
Тангенциальное ускорение
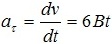
Нормальное ускорение
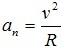
Полное ускорение
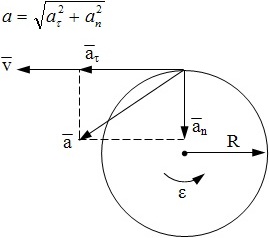
В момент времени t = 3 c
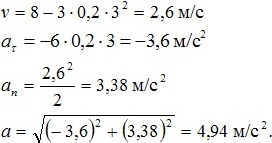 Ответ:
Ответ: v = 2,6 м/с; а
τ = −3,6 м/с
2; а
n = 3,38 м/с
2; а = 4,94 м/с
2.
10507
Диск радиусом R = 0,2 м вращается согласно уравнению φ = А+Bt+Ct3, где А = 3 рад; B = –1 рад/с; С = 0,1 рад/с3. Определить тангенциальное aτ, нормальное an и полное а ускорения точек на окружности диска для момента времени t = 10 с.
10508
По дуге окружности радиуса R = 10 м вращается точка. В некоторый момент времени нормальное ускорение точки an = 4,9 м/с2, вектор полного ускорения образует в этот момент с вектором нормального ускорения угол α = 60°. Найти скорость v и тангенциальное ускорение aτ точки.
13018
Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением аn = А + Bt + Ct2 (А = 1 м/с2, В = 6 м/с3, С = 9 м/с4). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t1 = 5 с после начала движения; 3) полное ускорение для момента времени t2 = 1 с.
40000
Колесо с радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = 5+t+2t2+t3 рад. Для точек, лежащих на ободе колеса, определить угловую скорость, угловое, нормальное, тангенциальное и полное ускорения к концу второй секунды. Какой угол образует вектор полного ускорения и вектор линейной скорости?
40124
Точка движется по окружности радиусом 4 м. Закон ее движения выражается уравнением s = 8 – 2t2, м. Определить: а) в какой момент времени нормальное ускорение точки будет равно 9 м/с2; б) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени?
40559
Точка движется по окружности радиусом R = 8 м. В некоторый момент времени нормальное ускорение точки равно 4 м/с2, вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60°. Найти линейную скорость и тангенциальное ускорение точки.
40639
Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.
40658
Точка вращается по кругу радиусом R = 1,2 м. Уравнение движения точки φ = Аt + Вt3, где А = 0,5 рад/с; В = 0,2 рад/с3. Определить тангенциально аτ, нормальное an и полное а ускорения точки в момент времени t = 4 с.
14458
Точка движется по окружности так, что зависимость пути от времени дается уравнением s = A–Bt+Ct2, где В = 2 м/с и С = 1 м/с2. Найти линейную скорость v точки, ее тангенциальное аτ, нормальное аn и полное а ускорения через время t = 3 с после начала движения, если известно, что при t' = 2 с нормальное ускорение точки а'n = 0,5 м/с2.
11012
Точка движется по окружности радиусом R = 8,00 м. В момент времени t1 нормальное ускорение точки аn = 4,00 м/с2;, а вектор полного ускорения а образует с вектором нормального ускорения аn угол α = 50,0°. Найти скорость v и тангенциальное ускорение аτ точки в этот момент времени t1.
11013
Точка движется по окружности радиусом R = 2 м согласно уравнению ξ = At3, где A = 2 м/с3. В какой момент времени t нормальное ускорение аn точки будет равно тангенциальному аτ. Определить полное ускорение а в этот момент.
26687
Колесо радиусом 0,3 м вращается согласно уравнению φ = 5–2t+0,3t2. Найти нормальное, тангенциальное и полное ускорение точек на ободе колеса через 5 с после начала движения.
26707
Закон движения материальной точки по окружности радиусом 2м выражается уравнением: S = 12-3t2 . Найти: 1) в какой момент времени нормальное ускорение точки будет равно 36 м/с2; 2) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени.
12267
Нормальное ускорение точки, движущейся по окружности радиусом 4 м, задается уравнением an = At3 (A = 0,5 м/с5). Определить: 1) тангенциальное ускорение точки в момент времени 5 c; 2) путь, пройденный точкой за время 5 с после начала движения; 3) полное ускорение для момента времени 1 с.
12612
Используя данные предыдущей задачи, определить: 1) частоту вращения диска в момент времени t2 в об/с и об/мин; 2) в момент времени t2 Определить скорость, нормальное, тангенциальное и полное ускорение точек, находящихся на расстоянии 10 см от оси вращения.
Данные из предыдущей задачи: t2 = 15 с; ω(t2) = 11,8 рад/с; β(t2) = 1,1 рад/с2.
Предыдущая задача: Диск вращается согласно уравнению φ = а + bt + ct2 + dt3, где φ — угол поворота радиуса в радианах, t — время в секундах. Определить угловую скорость и ускорение в моменты времени t1 = 11 с и t2 = 15 с. Каковы средние значения угловой скорости и углового ускорения в промежутке времени от t1 = 11 до t2 = 15 с включительно, если для Вашего варианта а = 1, b = 2 с–1, с = 0,1 с–2, d = 0,01 с–3?
13816
Точка движется по кругу так, что зависимость пути от времени задается уравнением: S = А + Bt +Ct2, где В = –2 м/с и С = 1 м/с2. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение в момент времени 2 с составляет 0,5 м/с2.
14141
Найти нормальное, тангенциальное и полное ускорение электрона на произвольной стационарной орбите в ионе Не+.
15622
Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S = 10+10t+0,5t2 (путь — в метрах, время — в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.
19975
Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t2, м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?
23836
Тело движется по окружности радиуса R = 2 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 0,1 рад, B = 0 рад/с, C = 0 рад/с2, D = 0,001 рад/с3. Для момента времени t = 6 с Определите: а) угол поворота φ, пройденный путь s и перемещение |Δr|; б) угловую и линейную скорости; в) угловое, тангенциальное, нормальное и полное ускорения.
23976
За время Δt = 0,4 с скорость тела изменилась от V1 = 14 м/с до V2 = 20 м/с и вектор скорости повернулся на угол α = 5°. Определить средние значения полного, нормального и тангенциального ускорения за этот интервал времени. Задачу решить графически. Графическое построение выполнить в масштабе: в 1 см - 2 м/с. Рассчитать радиус кривизны траектории.
24350
Точка движется по кривой так, что ее координаты на плоскости описываются уравнениями: X = A1 + B1t + С1t3, Y = А2 + B2t + С2t2, где A1 = 3 м, B1 = 0,5 м/с, C1 = 0,1 м/с2, A2 = 2 м, B2 = 0,3 м/с, C2 = 0,8 м/с2. Найдите скорость, полное, нормальное и тангенциальное ускорения точки в момент времени t = 2 с. Постройте следующие зависимости: v(t), an(t), aτ(t), a(t).
24351
Твердое тело вращается с угловым ускорением ε и начальной угловой скоростью ω0. Через время t после начала вращения вектор полного ускорения точки тела, находящейся на расстоянии R = 5 м от оси, составляет угол α = 30° с направлением скорости; vt и ωt — линейная и угловая скорости в этот момент времени; а, ап = 0,8 м/с2 и аτ соответственно полное, нормальное и тангенциальное ускорения в этот момент времени. Найти ε.
24484
Материальная точка движется по окружности радиусом r = 2 м согласно уравнению j = at+bt3, где a = 8 рад/с, b = -0,2 рад/с3. Найти тангенциальное, нормальное и полное ускорения в момент времени t = 3 с.
24689
Материальная точка массой 1 г движется по окружности радиуса 2 м согласно уравнению S = 8t – 0,2t3. Найти угловую и линейную скорость точки, тангенциальное, нормальное и полное ускорение точки в момент времени t = 2 с.
25015
Тело движется по окружности радиуса R = 0,8 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t)=A+Bt+Ct2+Dt3, где A = 0 рад, B = 0,1 рад/с, C = 0 рад/с2, D = 0,02 рад/с3. Для момента времени t = 2 с Определите:
а) Угол поворота φ, пройденный путь s и перемещение ❘Δr❘.
б) Угловую и линейную скорости.
Угловое, тангенциальное, нормальное и полное ускорения.
25016
Тело движется по окружности радиуса R = 0,9 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 0,2 рад, B = 0,01 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для момента времени t = 4 с Определите:
а) угол поворота φ, пройденный путь s и перемещение |Δr|;
б) угловую и линейную скорости;
в) угловое, тангенциальное, нормальное и полное ускорения.
25017
Тело движется по окружности радиуса R = 3 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t)=A+Bt+Ct2+Dt3, где A = 0,2 рад, B = 0 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для момента времени t = 8 с Определите:
а) Угол поворота φ, пройденный путь s и перемещение ❘Δr❘.
б) Угловую и линейную скорости. в) Угловое, тангенциальное, нормальное и полное ускорения.
25018
Тело движется по окружности радиуса R = 0,4 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t)=A+Bt+Ct2+Dt3, где A = 0 рад, B = –0,2 рад/с, C = 0,01 рад/с2, D = 0 рад/с3. Для момента времени t = 4 с Определите:
а) Угол поворота φ, пройденный путь s и перемещение ❘Δr❘.
б) Угловую и линейную скорости.
Угловое, тангенциальное, нормальное и полное ускорения.
25019
Тело движется по окружности радиуса R = 1 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 1 рад, B = 0,2 рад/с, C = –0,01 рад/с2, D = 0 рад/с3. Для момента времени t = 10 с Определите:
а) угол поворота φ, пройденный путь s и перемещение |Δr|;
б) угловую и линейную скорости;
в) угловое, тангенциальное, нормальное и полное ускорения.
25020
Тело движется по окружности радиуса R = 1 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 0 рад, B = 0,1 рад/с, C = 0,02 рад/с2, D = 0 рад/с3. Для момента времени t = 10 с Определите:
а) угол поворота φ, пройденный путь s и перемещение |Δr|;
б) угловую и линейную скорости;
в) угловое, тангенциальное, нормальное и полное ускорения.
25021
Тело движется по окружности радиуса R = 2 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 1 рад, B = 0 рад/с, C = 0 рад/с2, D = 0,002 рад/с3. Для момента времени t = 10 с Определите:
а) угол поворота φ, пройденный путь s и перемещение |Δr|;
б) угловую и линейную скорости;
в) угловое, тангенциальное, нормальное и полное ускорения.
26723
Тело движется по окружности радиуса R = 0,6 м так, что угол поворота φ зависит от времени в соответствии с уравнением φ(t) = A+Bt+Ct2+Dt3, где A = 0 рад, B = 0,2 рад/с, C = 0 рад/с2, D = 0,001 рад/с3. Для момента времени t = 4 с определите:
а) угол поворота φ, пройденный путь s и перемещение |Δr|;
б) угловую и линейную скорости;
в) угловое, тангенциальное, нормальное и полное ускорения.
25462
Тело движется по закругленному участку пути с радиусом кривизны R = 100 м по закону s = A + Bt + Ct2, где А = 50 м, B = 26 м/с, C = –1,5 м/с2. Найти скорость тела, его тангенциальное, нормальное и полное ускорения через t = 2 с после начала движения.