10545
Тонкий стержень длиной l = 40 см и массой m = 0,6 кг вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня φ = At+Bt³, где А = 1 рад/с; B = 0,1 рад/с³. Определить вращающий момент М в момент времени t = 2 с.

40148
Стержень массой 6 кг и длиной 40 см вращается вокруг оси, проходящей через середину, перпендикулярно длине стержня. Угол поворота изменяется во времени по закону φ = 3t³ – t² + 4t + 6. Определить вращающий момент, действующий на стержень через 2с после начала вращения.

40501
Определите момент инерции системы, состоящей из тонкого однородного стержня массой m = 100 г и длиной l = 80 см и двух шаров массами m₁ = 400 г и m₂ = 300 г, если первый шар закреплен на середине стержня, а второй — на его конце. Ось вращения перпендикулярна стержню и проходит через его свободный конец. Шары считать материальными точками.

40695
Стержень массой 6 кг и длиной 40 см вращается вокруг оси, проходящей через его середину перпендикулярно длине стержня. Угол поворота стержня изменяется со временем по закону φ = 3t³–t²+4t+6. Найти закон изменения момента сил, действующих на стержень. Каков момент сил через 3 с?

70207
На деревянный цилиндр, имеющий основание радиусом 31 см и высоту 27 см, намотаны два взаимно перпендикулярных витка с одинаковыми токами 78 А. Витки проходят через центры оснований. Найти напряженность магнитного поля в середине оси цилиндра.

40707
Два маленьких шарика массами m₁ = 0,4 кг и m₂ = 0,2 кг закреплены на концах невесомого стержня длиной l = 1 м. Определить момент инерции данной системы относительно поперечной оси, проходящей через середину стержня.

40723
Пуля массой 10 г, летящая со скоростью 600 м/с перпендикулярно стержню массой 1 кг, длиной 50 см на оси, проходящей через его середину, относительно которой стержень может свободно вращаться, попадает в конец стержня застревает в нем. Найти частоту вращения стержня.

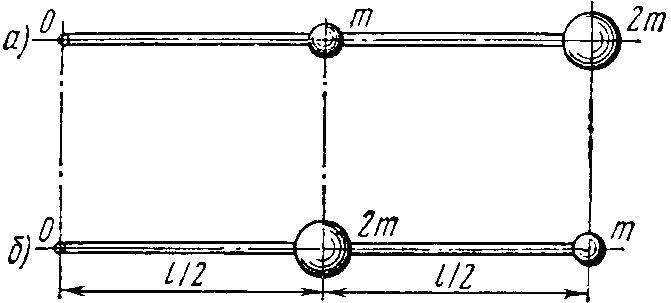
11134
Два шара массами m и 2m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рисунке. Определить моменты инерции J системы относительно оси, перпендикулярной стержню и проходящей через его конец в этих двух случаях. Размерами шаров пренебречь.

11137
Определить момент инерции J тонкого однородного стержня длиной l = 30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины.

11152
Тонкий однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением ε = 3 рад/с² около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М.

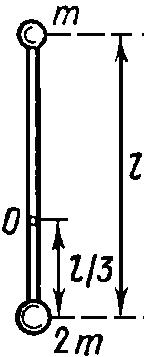
26164
На концах тонкого однородного стержня длиной l и массой 3m прикреплены маленькие шарики массами m и 2m. Определить момент инерции J такой системы относительно оси, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня. При расчетах принять l = 1 м, m = 0,1 кг. Шарики рассматривать как материальные точки.

26329
Деревянный стержень с массой 1000 г и длиной 40 см может вращаться около оси, проходящей через его середину перпендикулярно к стержню. В конец стержня попадает пуля с массой 10 г, летящая перпендикулярно к оси и к стержню со скоростью 200 м/с. Определить угловую скорость, которую получит стержень, если пуля застрянет в нем.

26447
Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M = 0,1 Н·м около оси, проходящей через точку, находящуюся на расстоянии l = 0,25 м от середины стержня перпендикулярно к его длине. Определить угловое ускорение стержня.

11780
По тонкому стержню длиной l = 20 см равномерно распределен заряд Q = 240 нКл. Стержень приведен во вращение с постоянной угловой скоростью ω = 10 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Определить: 1) магнитный момент p_m, обусловленный вращением заряженного стержня; 2) отношение магнитного момента к моменту импульса (p_m/L) если стержень имеет массу m = 12 г.

15564
Тонкий стержень длиной 50 см и массой 400 г вращается с угловым ускорением 6 рад/с. квад. около оси, проходящей через середину стержня перпендикулярно к нему. Определить вращающий момент.

17300
Тонкий однородный стержень вращается около оси, проходящей через его середину перпендикулярно к нему. В некоторый момент времени стержень разделяется на две равные части, которые продолжая вращаться, удаляются друг от друга. Принимая отделившиеся части за однородные стержни вдвое меньшей длины и пренебрегая работой, совершаемой при разделении, показать, что сумма моментов количества движения половинок стержня равна моменту количества движения стержня до разделения.

17801
Однородный магнитный стержень длиной l = 10 см, массой m = 6 г, магнитным моментом р_т = 2,1·10^–3 А·м² совершает гармонические колебания в однородном магнитном поле индукцией В = 1,5·10^–3 Тл. Ось колебаний перпендикулярна стержню и проходит через его середину. В положении равновесия направления магнитного поля и магнитного момента стержня совпадают. Определить период колебаний стержня и циклическую частоту. Пренебрегая моментом сил трения, записать дифференциальное уравнение гармонических колебаний и его решение с числовыми коэффициентами для углового смещения φ(t), выбрав произвольно величину начальной фазы колебаний α₀, считать, что амплитуда φ_m = 0,17 рад.

17802
Однородный магнитный стержень длиной l = 10 см, массой m = 6 г, магнитным моментом р_т = 2,1·10^–3 А·м² совершает гармонические колебания в однородном магнитном поле индукцией В = 1,5·10^–3 Тл. Ось колебаний перпендикулярна стержню и проходит через его середину. В положении равновесия направления магнитного поля и магнитного момента стержня совпадают. Cчитать, что амплитуда φ_m = 0,17 рад. 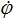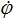Момент сил сопротивления М_с = –r, где r = 3·10^–7 кг·м²/с — коэффициент пропорциональности, = dφ/dt — угловая скорость колебаний ω_кол. Составить дифференциальное уравнение колебаний стержня, записать его решение, найти период затухающих колебаний, циклическую частоту и постоянную времени релаксации процесса.

20075
На концах тонкого однородного стержня длиной 30 см и массой 400 г закреплены грузы массой 200 и 300 г. Определить момент инерции этого физического маятника и период его собственных колебаний относительно оси, проходящей через середину стержня.

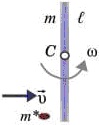
21190
Деревянный стержень массой m = 2 кг и длиной l = 1 м подвешен на оси, проходящей через его середину (точка С) перпендикулярно стержню. В конец стержня попадает пуля массой m* = 10 г, летящая перпендикулярно стержню и оси вращения со скоростью v = 500 м/с, и застревает в нём. Определить угловую скорость ω, с которой начнёт вращаться стержень.

23409
Однородный стержень длиной l = 1,5 м и массой M = 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой m = 10 г, летящая в горизонтальном направлении со скоростью V = 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?

10287
Заряд Q = 0,1 мкКл равномерно распределен по стержню длиной l = 50 см. Стержень вращается с угловой скоростью ω = 20 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент р_m, обусловленный вращением стержня.

10291
По тонкому стержню длиной l = 40 см равномерно распределен заряд Q = 60 нКл. Стержень вращается с частотой n = 12 с^-1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии a = l/3 от одного из его концов. Определить магнитный момент р_m, обусловленный вращением, стержня.

10767
По тонкому стержню длиной l = 20 см равномерно распределен заряд q = 240 нКл. Стержень приведен по вращение с постоянной угловой скоростью ω = 10рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Определить: 1) магнитный момент р_м, обусловленный вращением заряженного стержня; 2) отношение магнитного момента к моменту импульса (р_м/L), если стержень имеет массу m = 12 г.