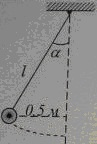11135
Три маленьких шарика массой m = 10 г каждый расположены в вершинах равностороннего треугольника со стороной а = 20 см и скреплены между собой. Определить момент инерции J системы относительно оси: 1) перпендикулярной плоскости треугольника и проходящей через центр описанной окружности; 2) лежащей в плоскости треугольника и проходящей через центр описанной окружности и одну из вершин треугольника. Массой стержней, соединяющих шары, пренебречь.

11136
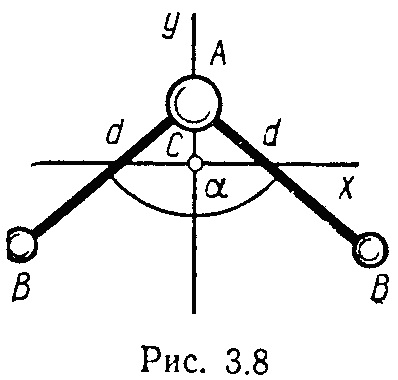
Определить моменты инерции J_x, J_y, J_z трехатомных молекул типа АВ₂ относительно осей x, у, z, проходящих через центр инерции C молекулы (ось z перпендикулярна плоскости xy). Межъядерное расстояние AB обозначено d, валентный угол α. Вычисления выполнить для следующих молекул: 1) H₂O (d = 0,097 нм, α = 104° 30'); 2) SO₂ (d = 0,145нм, α = 124°).

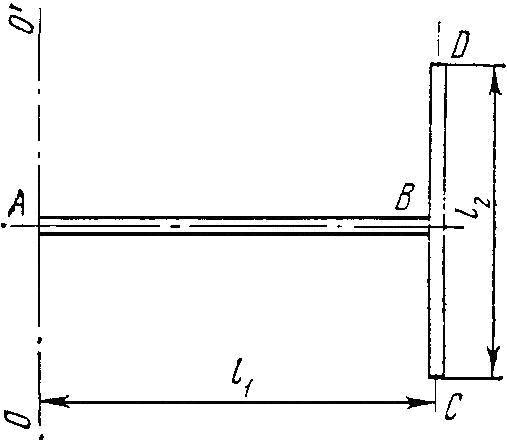
11141
Два однородных тонких стержня: АВ длиной l₁ = 40 см и массой m₁ = 900 г и CD длиной l₂ = 40 см и массой l₂ = 400 г скреплены под прямым углом. Определить момент инерции J системы стержней относительно оси OO', когда ось OO' проходит через точку А перпендикулярно плоскости чертежа.

26574
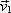
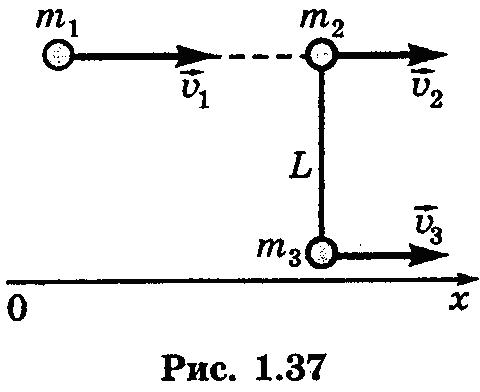
По условию задачи 10.25 Определите момент инерции и угловую скорость системы после удара относительно оси, проходящей через центр масс системы и перпендикулярной плоскости, в которой движутся шары. 10.25. Шар массой m₁, двигавшийся со скоростью = {v_1x, 0, 0}, испытал лобовое абсолютно неупругое соударение с одним из шаров жесткой гантели, как показано на рис. 1.37. v_1x = 1 м/с; v_2x = –2 м/с; v_3x = –2 м/с; m₁ = 2 кг; m₂ = 1 кг; m₃ = 3 кг; L = 0,6 м.

26629
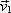
По условию задачи 10.8 Определите момент инерции и угловую скорость системы после удара относительно оси, проходящей через центр масс системы и перпендикулярной плоскости, в которой движутся шары. 10.8. Шар массой m₁, двигавшийся со скоростью = {v_1x, 0, 0}, испытал лобовое абсолютно неупругое соударение с одним из шаров жесткой гантели, как показано на рис. 1.37. v_1x = 1 м/с; v_2x = –1 м/с; v_3x = 0 м/с; m₁ = 2 кг; m₂ = 1 кг; m₃ = 2 кг; L = 1,0 м.

11606
Прямолинейный проводник с током I = 5 A и длинной l = 1 м вращается со скоростью ω = 50 c^–1 в плоскости, перпендикулярной магнитному полю, относительно оси, проходящей через конец проводника. Напряженность магнитного поля 500 А/м. Определите работу, совершаемую сторонними силами при вращении проводника за время t = 5 мин.

12400
Стержень длиной 1 м несет равномерно распределенный заряд 10 мКл. Он вращается относительно оси, проходящей через середину, с частотой 120 об/мин. Плоскость вращения перпендикулярна вектору магнитной индукции. Определить магнитный момент этого стержня.

16125
Груз массой 2 кг подвешен на нити длиной 1 м. Определить направление и модуль момента силы тяжести стержня относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке.

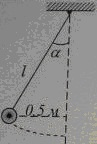
17870
Два круговых витка, первый радиусом 0,2 м, второй радиусом 0,3 м, расположены в параллельных плоскостях так, что прямая, соединяющая их центры, перпендикулярна их плоскостям. Расстояние между их центрами равно 0,5 м. По второму витку проходит ток равный 1 А. Какой ток должен идти по первому витку, чтобы магнитное поле в точке, лежащей на оси витков, на расстоянии 0,3 м от его центра было равно нулю?

17871
Два круговых витка, первый радиусом r₁ = 2 м и второй радиусом r₂ = 3 м, расположены в параллельных плоскостях так, что прямая, соединяющая их центры, перпендикулярна этим плоскостям. Расстояние между их центрами h = 8 м. По второму витку проходит ток I₂ = 1 А. Какой ток должен проходить по первому витку, чтобы магнитное поле в точке, лежащей на оси витков на равном расстоянии от их центров, было равно нулю?

18238
Электромагнитная волна в вакууме описывается уравнением E = E₀cos(ωt–kx), H = H₀cos(ωt–kx). Волна отражается от плоскости, перпендикулярной к оси X, без потери энергии. Написать уравнение, описывающее отраженную волну.

21917
Найти тензор инерции тонкой прямоугольной пластины массы М со сторонами а и b относительно осей, проходящих через центр масс пластины. Оси х и у параллельны сторонам пластины, ось z перпендикулярна плоскости пластины.

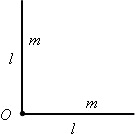
24048
Система состоит из двух тонких стержней массой m и длиной l каждый, скрепленных между собой, как показано на рисунке. Найдите момент инерции этой системы относительно оси, проходящей через точку О перпендикулярно плоскости рисунка. Изменится ли момент инерции этой системы, если угол между стержнями увеличить.

24171
Найдите момент инерции тонкого кольца относительно оси, перпендикулярной плоскости кольца и проходящей через любую точку его окружности. Масса кольца m, радиус кольца R.

24723
Момент инерции тонкого обруча массой m, радиусом R относительно оси, проходящей через центр обруча перпендикулярно плоскости, в которой лежит обруч, равен J = mR². Как изменится момент инерции обруча, если ось вращения перенести параллельно в точку на обруче?

24854
Металлическое кольцо радиусом R имеет заряд q. Напряженность поля Е в центре кольца и на расстоянии а от центра вдоль оси, перпендикулярной плоскости кольца, равна:

24920
Четыре одинаковых тела массы m каждое расположены на плоскости в вершинах квадрата со стороной L. Чему равен момент инерции I этой системы относительно оси, проходящей через одно из тел этой системы перпендикулярно плоскости?

25055
Твердое тело является физическим маятником и может совершать колебания в вертикальной плоскости около горизонтальной оси, проходящей через точку О на нем. Определите: а) положение центра масс С маятника относительно точки O; б) момент инерции маятника J относительно горизонтальной оси, проходящей через точку О; в) период колебаний и приведенную длину маятника. Тело — однородное кольцо радиуса R = 40 см и массой 2m, на противоположных концах диаметра которого находятся грузы массами m и 2m. Положение точки О — на конце диаметра с меньшим грузом, перпендикулярно плоскости кольца.