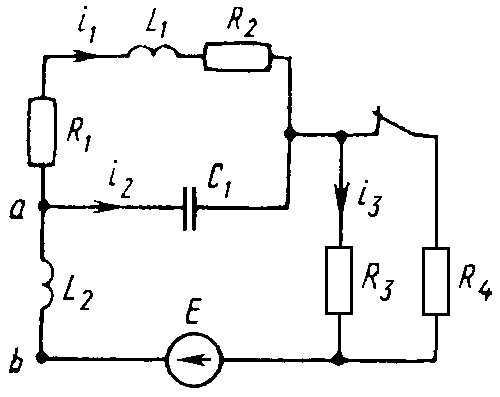
0692t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 100 мкФ
R₁ = 2 Ом
R₂ = 8 Ом
R₃ = 10 Ом
R₄ = 10 Ом
i₁ — ?

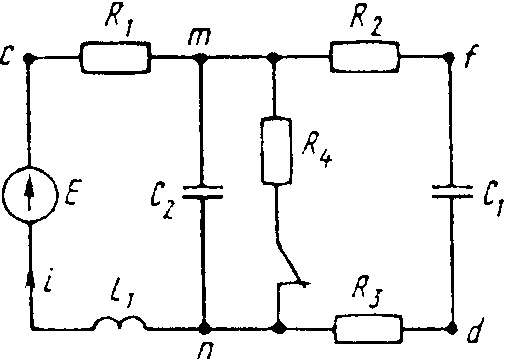
0693t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 20 Ом
R₃ = 0 Ом
R₄ = 2 Ом
U_L1 — ?

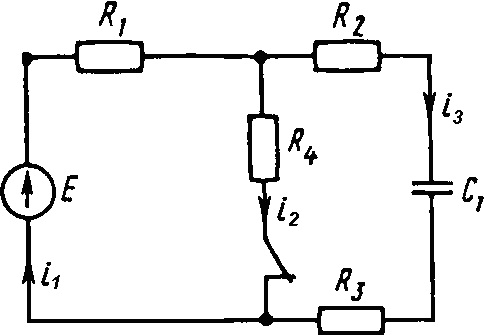
0694t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
С₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 20 Ом
R₃ = 0 Ом
R₄ = 2 Ом
i₁ — ?

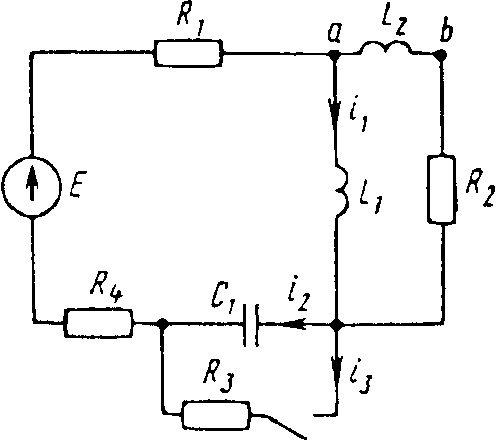
0695t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 2 мГн
C₁ = 5 мкФ
R₁ = 5 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 5 Ом
i₂ — ?

0696t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 2 мГн
C₁ = 5 мкФ
R₁ = 5 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 5 Ом
i₂ — ?

0697t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

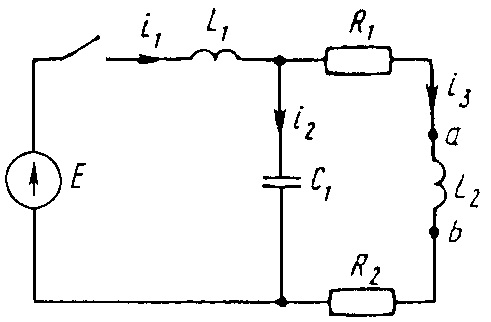
Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 1 Ом
R₂ = 3 Ом
i₃ — ?

0698t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

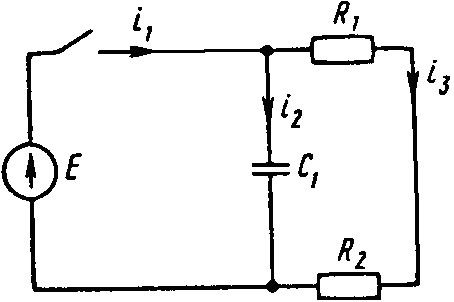
Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 1 Ом
R₂ = 3 Ом
i₃ — ?

0699t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

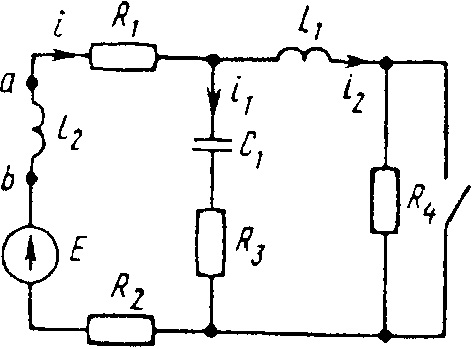
Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 1 Ом
R₄ = 1 Ом
i₂ — ?

0700t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

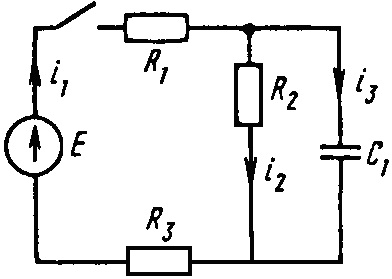
Е = 100 В
C₁ = 50 мкФ
R₁ = 3 Ом
R₂ = 8 Ом
R₃ = 5 Ом
R₄ = —
U_C — ?

0701t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

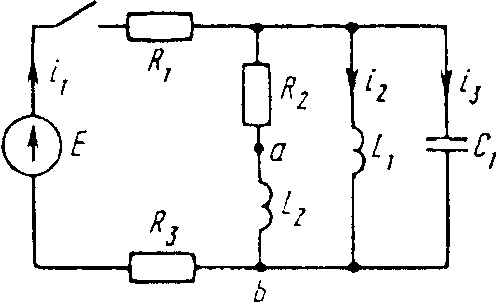
Е = 100 В
C₁ = 50 мкФ
R₁ = 3 Ом
R₂ = 8 Ом
R₃ = 5 Ом
R₄ = —
U_C — ?

0702t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

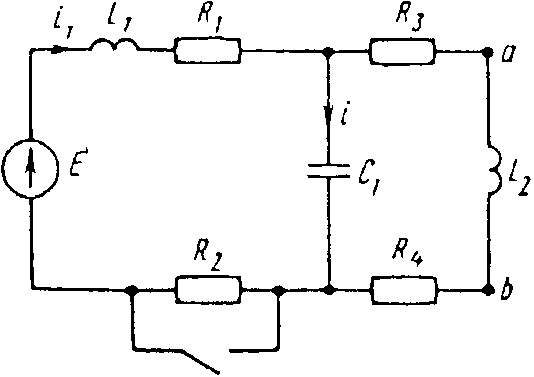
Е = 50 В
L₁ = 1 мГн
C₁ = 1500 мкФ
R₁ = 2 Ом
R₂ = 13 Ом
R₃ = 2 Ом
R₄ = 3 Ом
i — ?

0703t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 1500 мкФ
R₁ = 2 Ом
R₂ = 13 Ом
R₃ = 2 Ом
R₄ = 3 Ом
i — ?

0704t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

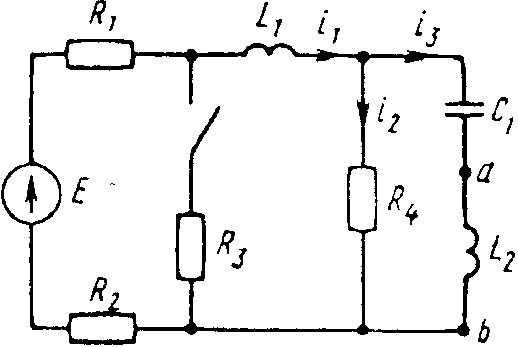
Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 80 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₃ — ?

0705t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

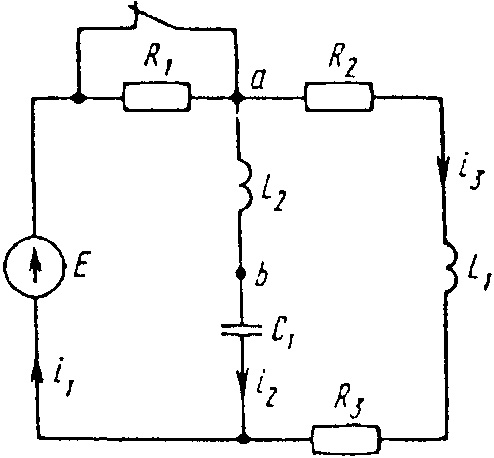
Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 50 Ом
R₂ = 20 Ом
R₃ = 30 Ом
R₄ = —
U_L1 — ?

0706t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

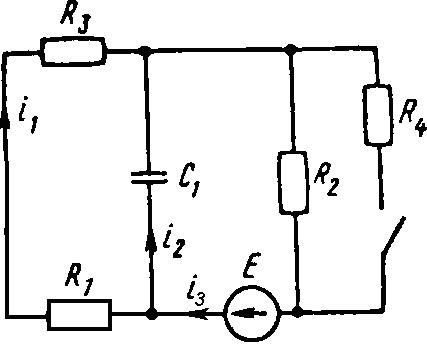
Е = 300 В
С₁ = 4 мкФ
R₁ = 15 Ом
R₂ = 20 Ом
R₃ = 5 Ом
R₄ = 20 Ом
i₂ — ?

0707t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

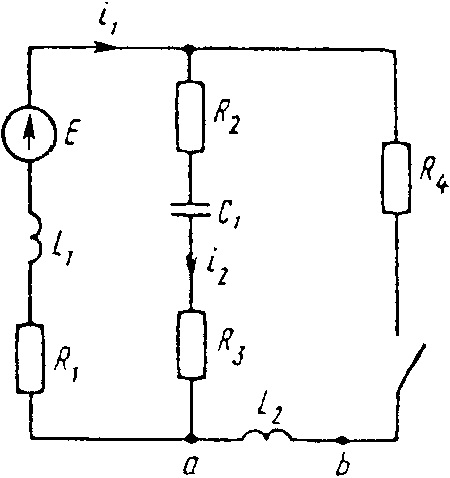
Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 17 Ом
R₃ = 3 Ом
R₄ = 2 Ом
U_L — ?

0708t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

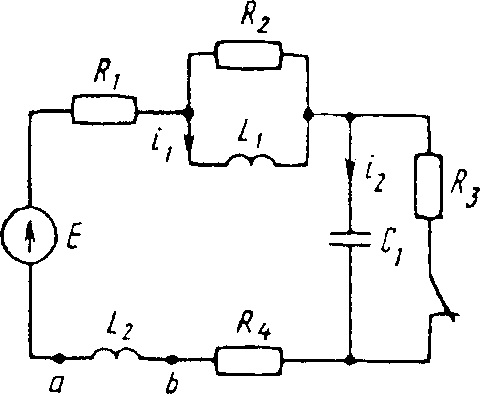
Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 9 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 1 Ом
U_L1 — ?

0709t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 9 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 1 Ом
U_L1 — ?

0710t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

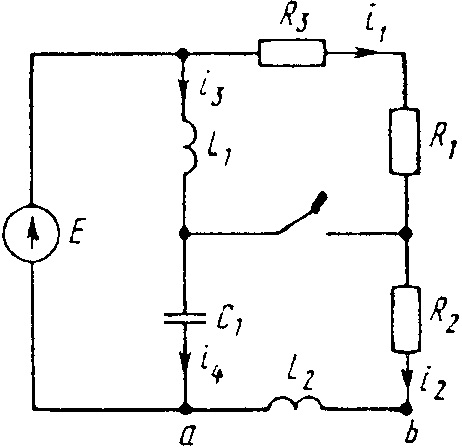
Е = 30 В
L₁ = 1 мГн
C₁ = 2,5 мкФ
R₁ = 5 Ом
R₂ = 10 Ом
R₃ = 15 Ом
R₄ = —
i₃ — ?

0711t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

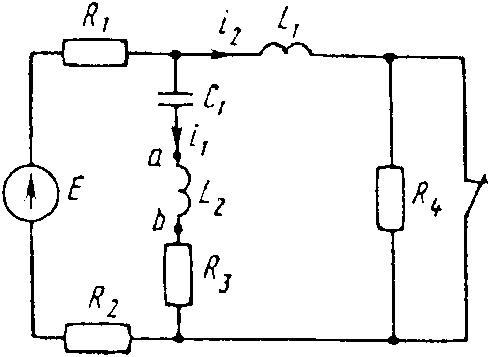
Е = 200 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 50 Ом
R₂ = 50 Ом
R₃ = 50 Ом
R₄ = 100 Ом
U_R3 — ?

0712t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

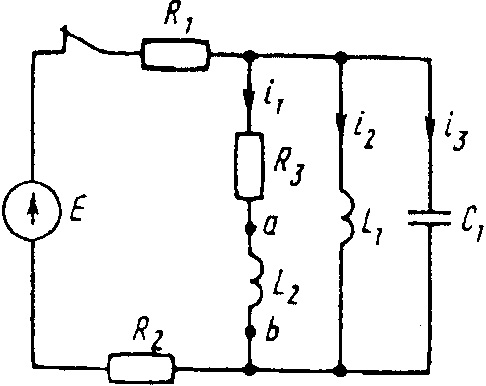
Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 5 Ом
R₂ = 15 Ом
R₃ = 4 Ом
R₄ = —
U_L1 — ?

0713t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

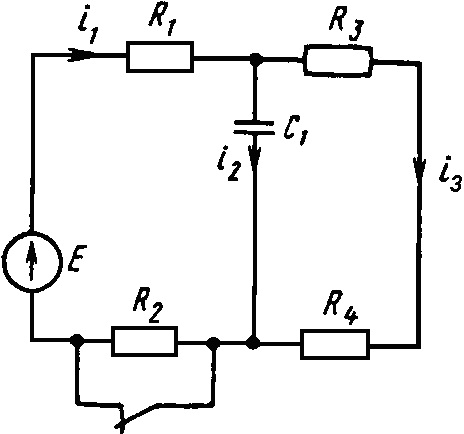
Е = 50 В
C₁ = 1670 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 2 Ом
R₄ = 4 Ом
i₂ — ?

0714t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

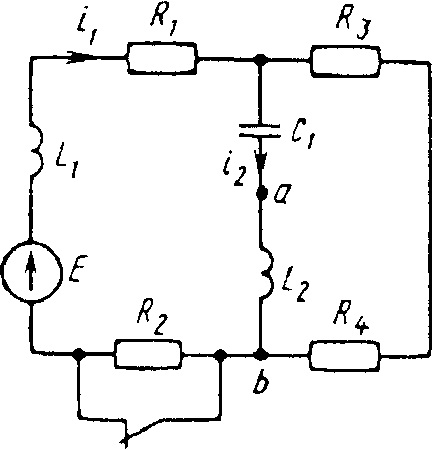
Е = 50 В
L₁ = 2 мГн
C₁ = 1670 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 2 Ом
R₄ = 4 Ом
i₂ — ?

0715t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

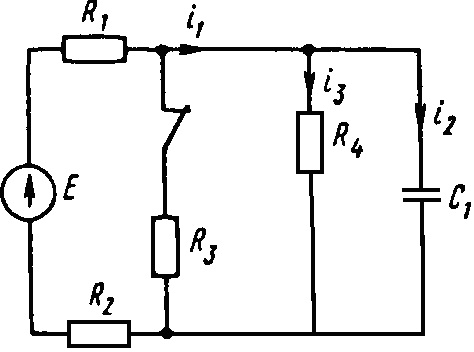
Е = 120 В
С₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 80 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₂ — ?

0716t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

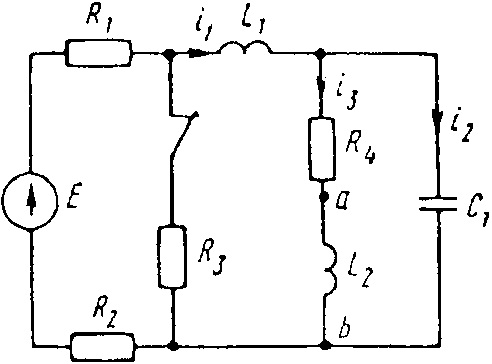
Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 80 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₂ — ?

0717t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

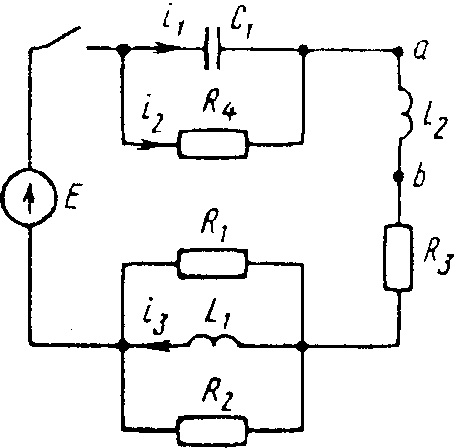
Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 12 Ом
R₂ = 6 Ом
R₃ = 8 Ом
R₄ = 4 Ом
i₃ — ?

0718t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 12 Ом
R₂ = 6 Ом
R₃ = 8 Ом
R₄ = 4 Ом
i₃ — ?

0719t
Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС E. Рассмотреть переходный процесс в цепи без катушек. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

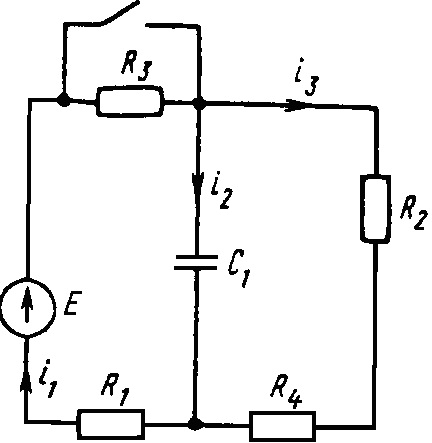
Е = 200 В
С₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 10 Ом
R₃ = 50 Ом
R₄ = 30 Ом
i₂ — ?

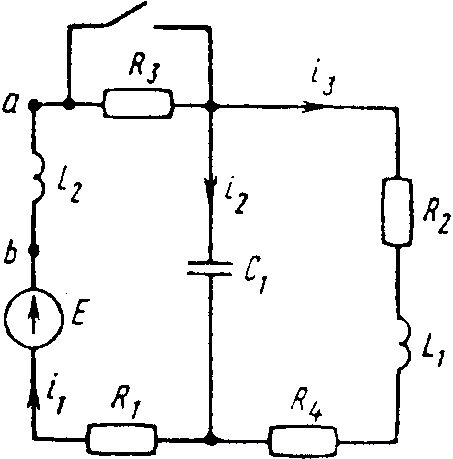
0720t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 10 Ом
R₃ = 50 Ом
R₄ = 30 Ом
i₂ — ?

0721t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 100 мкФ
R₁ = 3 Ом
R₂ = 7 Ом
R₃ = 10 Ом
R₄ = 10 Ом
i₂ — ?

0722t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 1500 мкФ
R₁ = 2 Ом
R₂ = 13 Ом
R₃ = 3 Ом
R₄ = 2 Ом
u_L — ?

0723t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 30 Ом
R₂ = 70 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₂ — ?

0724t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 30 Ом
R₂ = 70 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₂ — ?

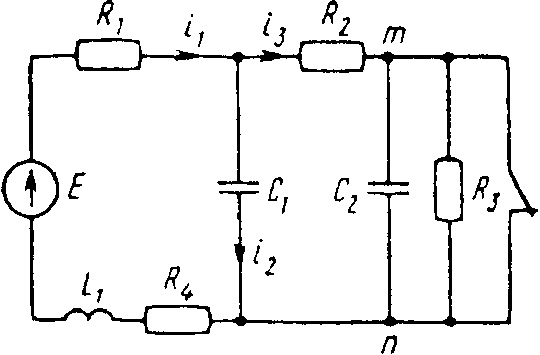
0725t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 1 мГн
C₁ = 50 мкФ
R₁ = 4 Ом
R₂ = 10 Ом
R₃ = 20 Ом
R₄ = 6 Ом
i₂ — ?

0726t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 50 Ом
R₂ = 10 Ом
R₃ = 40 Ом
R₄ = —
i₃ — ?

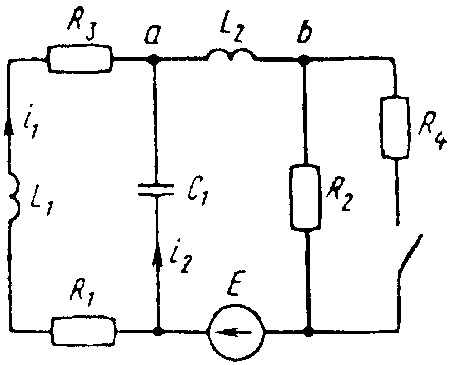
0727t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 300 В
L₁ = 5 мГн
C₁ = 4 мкФ
R₁ = 3 Ом
R₂ = 20 Ом
R₃ = 17 Ом
R₄ = 20 Ом
i₁ — ?

0728t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 8 Ом
R₃ = 12 Ом
R₄ = 2 Ом
U_L — ?

0729t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 0 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 10 Ом
I₁ — ?

0730t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 30 В
L₁ = 1 мГн
C₁ = 2,5 мкФ
R₁ = 15 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = —
i₄ — ?

0731t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 15 Ом
R₂ = 5 Ом
R₃ = 4 Ом
R₄ = —
i₃ — ?

0732t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 30 Ом
R₂ = 70 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₃ — ?

0733t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 100 мкФ
R₁ = 4 Ом
R₂ = 6 Ом
R₃ = 10 Ом
R₄ = 10 Ом
i₃ — ?

0734t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 3 Ом
R₂ = 1 Ом
U_L — ?

0735t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 3 Ом
R₂ = 1 Ом
U_L — ?

0736t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 1500 мкФ
R₁ = 2 Ом
R₂ = 13 Ом
R₃ = 4 Ом
R₄ = 1 Ом
U_C1 — ?

0737t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 40 Ом
R₂ = 60 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
u_L — ?

0738t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 50 Ом
R₂ = 30 Ом
R₃ = 20 Ом
R₄ = —
i₁ — ?

0739t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 20 Ом
R₂ = 11 Ом
R₃ = 9 Ом
R₄ = 2 Ом
U_C — ?

0740t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 30 В
L₁ = 1 мГн
C₁ = 2,5 мкФ
R₁ = 12 Ом
R₂ = 10 Ом
R₃ = 8 Ом
R₄ = —
i₂ — ?

0741t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 7 Ом
R₂ = 13 Ом
R₃ = 4 Ом
R₄ = —
i₂ — ?

0742t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 7 Ом
R₂ = 13 Ом
R₃ = 4 Ом
R₄ = —
i₂ — ?

0743t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 40 Ом
R₂ = 60 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
U_L — ?

0744t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 30 Ом
R₃ = 50 Ом
R₄ = 10 Ом
i₁ — ?

0745t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 100 мкФ
R₁ = 5 Ом
R₂ = 5 Ом
R₃ = 10 Ом
R₄ = 10 Ом
U_L — ?

0746t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 100 мкФ
R₁ = 5 Ом
R₂ = 5 Ом
R₃ = 10 Ом
R₄ = 10 Ом
U_L — ?

0747t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 2 мГн
C₁ = 5 мкФ
R₁ = 10 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 0 Ом
U_C — ?

0748t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 1 Ом
R₂ = 3 Ом
U_C1 — ?

0749t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 1 Ом
R₂ = 3 Ом
U_C1 — ?

0750t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 0 Ом
R₂ = 3 Ом
R₃ = 1 Ом
R₄ = 1 Ом
U_C — ?

0751t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 50 Ом
R₂ = 35 Ом
R₃ = 15 Ом
R₄ = —
i₂ — ?

0752t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 2 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 8 Ом
U_R1 — ?

0753t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 30 В
L₁ = 1 мГн
C₁ = 2,5 мкФ
R₁ = 8 Ом
R₂ = 10 Ом
R₃ = 12 Ом
R₄ = —
U_L — ?

0754t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 2 мГн
C₁ = 1670 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 5 Ом
R₄ = 1 Ом
U_R1 — ?

0755t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 2 мГн
C₁ = 1670 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 5 Ом
R₄ = 1 Ом
U_R1 — ?

0756t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 8 Ом
R₂ = 8 Ом
R₃ = 8 Ом
R₄ = 4 Ом
U_L — ?

0757t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 2 мГн
C₁ = 5 мкФ
R₁ = 8 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 2 Ом
i₁ — ?

0758t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 100 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 2 Ом
R₂ = 2 Ом
i₁ — ?

0759t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 3 Ом
R₂ = 0 Ом
R₃ = 1 Ом
R₄ = 1 Ом
i₁ — ?

0760t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 1 мГн
C₁ = 1500 мкФ
R₁ = 2 Ом
R₂ = 13 Ом
R₃ = 1 Ом
R₄ = 4 Ом
u_L — ?

0761t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 90 Ом
R₃ = 1000 Ом
R₄ = 1000 Ом
i₁ — ?

0762t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 300 В
L₁ = 5 мГн
C₁ = 4 мкФ
R₁ = 10 Ом
R₂ = 20 Ом
R₃ = 10 Ом
R₄ = 20 Ом
U_C1 — ?

0763t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 6 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 4 Ом
U_L1 — ?

0764t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 150 В
L₁ = 4 мГн
C₁ = 5 мкФ
R₁ = 6 Ом
R₂ = 10 Ом
R₃ = 5 Ом
R₄ = 4 Ом
U_L1 — ?

0765t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 30 В
L₁ = 1 мГн
C₁ = 2,5 мкФ
R₁ = 10 Ом
R₂ = 10 Ом
R₃ = 10 Ом
R₄ = —
U_C — ?

0766t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 100 Ом
R₂ = 0 Ом
R₃ = 50 Ом
R₄ = 100 Ом
i₁ — ?

0767t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 10 мГн
C₁ = 10 мкФ
R₁ = 100 Ом
R₂ = 0 Ом
R₃ = 50 Ом
R₄ = 100 Ом
i₁ — ?

0768t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 50 В
L₁ = 2 мГн
C₁ = 1670 мкФ
R₁ = 1 Ом
R₂ = 2 Ом
R₃ = 1 Ом
R₄ = 5 Ом
i₁ — ?

0769t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 120 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 8 Ом
R₂ = 8 Ом
R₃ = 8 Ом
R₄ = 4 Ом
i₁(t) — ?

0770t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 20 Ом
R₃ = 50 Ом
R₄ = 20 Ом
i₁ — ?

0771t
Дана электрическая цепь, в которой происходит коммутация (рис. 3.1—3.20). В цепи действует постоянная ЭДС E. Параметры цепи приведены в табл. 3.1. Рассмотреть переходный процесс в цепи второго порядка (см. рис. 3.1—3.20), когда L₂ = 0, т.е. участок a—b схемы закорочен, и когда C₂ = ∞, т.е. ветвь m—n с конденсатором C₂ разомкнута. При вычерчивании схемы элементы L₂ и C₂ должны отсутствовать. Определить закон изменения во времени указанной в таблице величины (тока или напряжения).
Задачу решить классическим методом. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 3/|p|_min, где |p|_min — меньший по модулю корень характеристического уравнения.

Е = 200 В
L₁ = 1 мГн
C₁ = 10 мкФ
R₁ = 10 Ом
R₂ = 20 Ом
R₃ = 50 Ом
R₄ = 20 Ом
i₁ — ?