Пример решения задачи 10010
Условие Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение аτ точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение an=2,7 м/с2.
Краткое условие
R = 30 см = 0,3 м
t = 4 с
аn = 2,7 м/с2
n = 3 оборота
ε = const
Найти
aτ ― ?
Решение
Напишем преобразования:
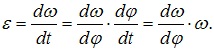
Разделим переменные и проинтегрируем:

В уравнении ε=dω/dt разделим переменные и проинтегрируем:
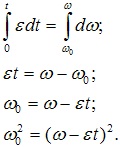
Подставим найденное выражение в уравнение (1).
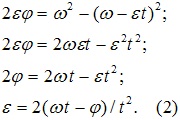
Найдём величины, входящие в уравнение (2), для момента времени t=4c.
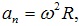
откуда
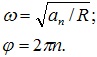
Подставим эти выражения в уравнение (2):
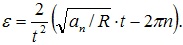
Тогда
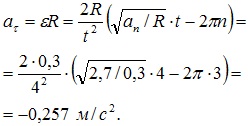
Ответ: an = 9,6 м/с2; aτ = –1,9 м/с2.
Условие Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение аτ точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение an=2,7 м/с2.
Краткое условие
R = 30 см = 0,3 м
t = 4 с
аn = 2,7 м/с2
n = 3 оборота
ε = const
Найти
aτ ― ?
Решение
Напишем преобразования:
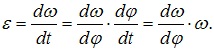
Разделим переменные и проинтегрируем:

В уравнении ε=dω/dt разделим переменные и проинтегрируем:
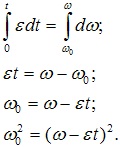
Подставим найденное выражение в уравнение (1).
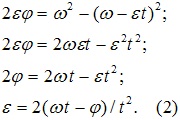
Найдём величины, входящие в уравнение (2), для момента времени t=4c.
откуда
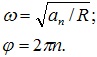
Подставим эти выражения в уравнение (2):
Тогда
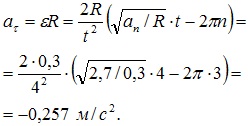
Ответ: an = 9,6 м/с2; aτ = –1,9 м/с2.