уравнение и построить траекторию точки
40708
Точка участвует в двух колебаниях поперечного направления х = Acosωt и y = Bsin(ω(t+τ)), где А = 5 см, В = 3 см, τ = 1 с, ω = π рад/с. Найти уравнение траектории y(x) результирующего колебания и построить его, указав направление движения точки вдоль траектории.
24211
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = A sin ωt, y = A cos 2ωt.
24212
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = A sin 2ωt, y = A sin 3ωt.
24213
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = A cos 3ωt, y = A cos 2ωt.
24221
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = A cos 3ωt, y = A sin ωt.
24222
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = 2A cos 2ωt, y = A cos 3ωt.
24227
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = A cos ωt, y = A sin 3ωt.
24228
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = 2A sin 3ωt, y = A sin 2ωt.
24234
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = 2A cos ωt, y = A cos 2ωt.
24235
Применяя графический метод сложения и соблюдая масштаб, постройте траекторию светящейся точки на экране осциллографа как результат сложения двух взаимно перпендикулярных колебаний x(t) и y(t), которые совершает эта точка.
x = 3A sin 3ωt, y = A cos 3ωt.
17496
Материальная точка двигается так, что ее координаты изменяются в зависимости от времени согласно уравнениям x = A·sin(ω·t); y = A·sin(2ω·t). Запишите уравнение траектории, постройте график у = f(x), определите скорость точки через t1 = 1 с, если А = 1 см, ω = π рад/c.
17510
Зависимости координат материальной точки по двум взаимно перпендикулярным направлениям описывается уравнениями: x(t) = 3sin 3t, y(t) = 6cos 3t, см. Вычислите: 1) зависимость скорости и ускорения от времени; 2) модули скорости и ускорения в момент времени t = 0,2 с; 3) максимальную скорость точки; 4) уравнение траектории движения точки у = f(x); 5) постройте график зависимости у = f(х) и Определите координаты точек траектории, в которых скорость точки наибольшая и наименьшая. Изобразите их на графике; 6) назовите характер движения точки.
19691
Точка движется в плоскости XY вдоль оси X равномерно со скоростью Vx = 0,5 м/с, а вдоль оси Y так, что уравнение траектории имеет вид y = 0,2x2 + 15x3. Найти зависимость скорости движения точки вдоль оси Y от времени, полагая, что при t = 0 точка находилась в начале координат.
20186
Уравнение движения материальной точки задается в параметрической форме: x = 4cos3πt, y = 4sin3πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 1 с до t2 = 4 с.
20188
Уравнение движения материальной точки задается в параметрической форме: x = 4cos3πt, y = 4sin3πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 2 с до t2 = 4 с.
20189
Уравнение движения материальной точки задается в параметрической форме: x = 2cos2πt, y = 2sin2πt. Построить траекторию движения материальной точки и найти путь и перемещение за время от t1 = 0,5 с до t2 = 3 с.
21832
Движение тела в поле Земли определяется уравнениями х(t) = 15t, y(t) = 30t–4,9t2, м. Вычислите:
1) зависимость проекций скорости и ускорения на оси OХ и OY от времени;
2) начальную и конечную скорости движения точки;
3) запишите уравнение траектории движения тела у = f(t), постройте график зависимости у = f(t) для моментов времени t1 = 0 с, t2 = tподъема, t3 = tпадения и назовите характер движения тела;
4) максимальную высоту подъема, дальность полета и модуль перемещения;
5) радиус кривизны в верхней точке траектории.
21988
На горизонтально и вертикально отклоняющие пластины осциллографа подаются соответственно напряжения UX = 20sin 100πt B, Uу = 25sin (100πt+π/6) В. Чувствительности пластин jx = jу = 2 мм/В. Написать уравнение траектории, описываемой электронным лучом на экране осциллографа. Найти время, через которое луч возвращается в исходную точку.
22750
Лампа висит над точкой А поверхности стола на высоте Н. Построить линию, при перемещении по которой лампа в точке А создает прежнюю освещенность.
23224
Движение материальной точки в плоскости задано уравнениями х = A1sin ωt, у = A1sin(ωt+π), где A1 = 2·10–2 м, A2 = 4·10–2 м. Построить уравнение траектории и начертить график.
23265
Даны параметрические уравнения движения материальной точки: х = 3R·sin(ωt); у = R·cos(ωt). Определить траекторию движения точки и ее ускорение, если R = 10 м, ω = π рад/c.
23535
Движение тела в поле Земли определяется уравнениями x(t) = 10t, y(t) = 20t–4,9t2, м. Вычислите: 1) зависимость проекций скорости и ускорения на оси OX и OY от времени; 2) начальную и конечную скорости движения; 3) уравнения траектории движения тела y = f(t) и постройте график зависимости y = f(t) для моментов времени t1 = 0 c, t2 = tподъема, t3 = tпадения, назовите характер движения тела. 4) максимальную высоту подъема, дальность полета и модуль перемещения; 5) радиус кривизны в верхней точке траектории.
25048
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=3 см, B=2 см, α1=0 рад, α2=π/2 рад, ω1=2π рад/с, ω2=2π рад/с, t=0,25 с.
а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
25049
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=2 см, B=2 см, α1=0 рад, α2= –π/2 рад, ω1= 2π рад/с, ω2= 2π рад/с, t=0,25 с.
а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
25050
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=1 см, B=2 см, α1=0 рад, α2= 0 рад, ω1=π рад/с, ω2=π рад/с, t=0,5 с.
а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
25174
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=2 см, B=1 см, α1=0 рад, α2=π рад, ω1=π рад/с, ω2=π рад/с, t=0,25 с. а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
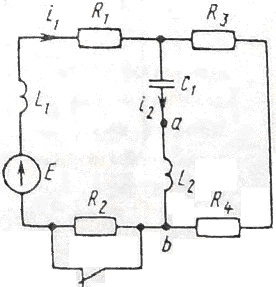
0523tДана электрическая цепь, в которой происходит коммутация (4-1—4-20). В цепи действует постоянная э.д.с. E. Параметры цепи приведены в табл. 4-1. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком-либо элементе или между заданными точками схемы.
Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени на интервале от t=0 до t=3/|p|
мин. Здесь |p|
мин — меньший по модулю корень характеристического уравнения.
E=50 В
L=2 мГн
C=1670 мкФ
R1=1 Ом
R2=2 Ом
R3=1 Ом
R4=5 Ом
i1(t) — ?
26725
Точка движется по плоскости так, что ее координаты зависят от времени в соответствии с уравнениями x(t)=Acos(ω1t+α1) и y(t)=Bcos(ω2t+α2), где A=1 см, B=3 см, α1=0 рад, α2=0 рад, ω1=π рад/с, ω2=2π рад/с, t=0,5 с.
а) Получите уравнение траектории точки и постройте ее с соблюдением масштаба; б) Определите координаты точки, ее скорость и ускорение в момент времени t; в) Укажите на рисунке положение точки, направления ее скорости и ускорения в начальный момент времени и в момент времени t.
