10007
Материальная точка движется по окружности с постоянной угловой скоростью v₀=π/6 рад/с. Во сколько раз путь Δs, пройденный точкой за время t=4 с, будет больше модуля ее перемещения Δr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол φ₀=π/3 рад.

13023
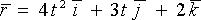
Радиус-вектор материальной точки изменяется со временем по закону Определите: 1) скорость v; 2) ускорение а; 3) модуль скорости в момент времени t = 2 с.

40703
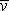
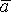
Радиус-вектор материальной точки изменяется со временем по закону где А = 2 м/с²; В = 5 м/с; С = 3 м. Определить: 1) скорость ; 2) ускорение ; 3) модуль скорости v в момент времени t = 4 с.

40799
Система состоит из трех частиц m₁ = 1,0 кг, m₂ = 0,2 кг, m₃ = 0,3 кг. Первая частица находится в точке с координатами (1,2,3), вторая — в точке (2,3,1) и третья — в точке (3,1,2). Определить выражение для радиус-вектора r_C центра масс системы.

26303
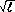
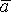
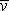
Материальная частица движется по дуге с радиусом R = 1,00 м. Ее скорость зависит от дуговой координаты l по закону v=k, где k — некоторая постоянная. Найти угол α между векторами полного ускорения и скорости точки в момент времени, когда ее дуговая координата l = 0,50 м.

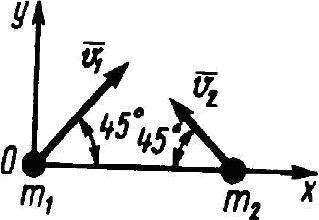
26596
Определить проекцию на ось Оу главного вектора количества движения системы двух материальных точек, массы которых т₁ = 4 кг, m₂ = 2 кг, в момент времени, когда их скорости v₁ = 2 м/с, v₂ = 1 м/с.

13303
Радиус-вектор материальной точки изменяется со временем по закону r = t³i+3t²j, где i, j — орты осей х и у. Определите для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения.

13304
Движение материальной точки в плоскости ху описывается законом х = At, y = At(1+Bt), где А и В — положительные постоянные. Определите: 1) уравнение траектории материальной точки у(х); 2) радиус-вектор r точки в зависимости от времени; 3) скорость v точки в зависимости от времени; 4) ускорение а точки в зависимости от времени.

13305
Материальная точка начинает двигаться по окружности радиусом r = 12,5 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с². Определите: 1) момент времени, при котором вектор ускорения а образует с вектором скорости v угол α = 45°; 2) путь, пройденный за это время движущейся точкой.

15304
Точка движется в плоскости так, что ее движение описывается уравнениями x = 3t; y = 3t(1+0,5t). Найти путь, пройденный материальной точкой за 2 секунды; модуль скорости в этот момент времени. Записать уравнение траектории движения материальной точки; уравнения радиус вектора; вектора скорости и вектора ускорения.

17617
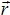
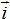
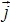
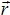
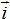
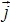
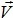
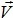
Материальная точка движется по плоскости. Движение точки в векторном виде описывается уравнением (t) = At³ + Bt ( — радиус-вектор, , — единичные орты соответственно по осям ОХ и OY). Написать зависимость вектора скорости от времени = (t). Найти в момент времени t = 1 с после начала движения: 1) модуль скорости; 2) модуль тангенциального ускорения; 3) модуль нормального ускорения; 4) модуль полного ускорения, если А = 0,1 м/с³, В = 1 м/с.

17688
Материальная точка начала движение из начала координат и движется так, что ее скорость зависит от времени по закону v₁ = (αt² + βt)i+ γt³j (м/с). Одновременно вторая точка начала движение и движется так, что радиус-вектор зависит от времени по закону r₂ = δt³i + θt⁴j (м), где α, β, γ, δ, θ — постоянные. Найти угол φ между ускорениями точек через промежуток времени τ после начала движения.

20143
Радиус-вектор материальной точки изменяется со временем по закону r = t³i + 3t²j. Определите модуль и вектор скорости и ускорения.

20205
Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а_τ = 0,4 см/с². Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 60°. Определить t.

20206
Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а_τ. Через промежуток времени t = 5,0 с вектор полного ускорения а образует с вектором мгновенной скорости v = 0,02 м/с угол β. Определить a.

20207
Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 30 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с². Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 45°. Определить v.

20208
Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R с постоянным тангенциальным ускорением а_τ. Через промежуток времени t = 6,5 с вектор полного ускорения а = 0,8 см/с² образует с вектором мгновенной скорости v = 0,03 м/с угол β. Определить β.

20209
Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 50 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с². Через промежуток времени t вектор полного ускорения а = 0,9 см/с² образует с вектором мгновенной скорости v угол β. Определить v.

20389
Материальная точка движется по окружности радиуса R, причем φ = ωt (φ – угол между радиус-вектором точки, проведенным из некоторой точки А окружности, и прямой, соединяющей точку А и центр окружности; ω — константа). Найти тангенциальную и нормальную составляющие скорости и ускорения точки.

21434
Вектор скорости материальной точки, оставаясь неизменным по величине, поворачивается за время t на 90°. Чему равна величина действующей на точку силы, если известно, что величина импульса точки равна р.

22878
Заданы начальное значения радиус–вектора r₁ = 4i–3j, м и конечное r₂ = –i–2j, м описывающие положения движущейся материальной точки для моментов времени t₁ = 1 c и t₂ = 3 c. Нарисуйте вектор перемещения рассматриваемой точки в координатах X-Y. Найдите величину средней скорости перемещения точки за этот интервал времен.

23141
Радиус-вектор материальной точки зависит от времени по закону r(t) = 2it – 4j + (1 + t²)k. Найти величину вектора силы, действующего на материальную точку в момент t = 2 сек. Масса материальной точки — 3 г.

23143
Радиус-вектор материальной точки в начальный момент времени r(0) = 2i – 4j + k, скорость зависит от времени по закону v(t) = 2ti – (4 – t)j + k. Найти величину перемещения материальной точки за время от t = 3 сек до t = 5 сек.

24167
К материальной точке, радиус – вектор которой относительно начала координат O равен r = 3i + 4j, приложена сила F = –2i + 1,5j. Вычислите момент M и плечо l силы F относительно точки O.

24768
Имеется кольцо радиусом R. Радиус проволоки равен r, плотность материала проволоки равна ρ. Найти силу F, с которой это кольцо притягивает материальную точку массой m, находящуюся на оси кольца на расстоянии l от его центра.