10916
Частица в потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках интервала (0<x<l) плотность вероятности нахождения частицы имеет максимальное и минимальное значения.

20224
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < х < l/4 на втором энергетическом уровне.

20225
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < х < l/2 на третьем энергетическом уровне.

90140
Частица в потенциальной яме шириной l находится в низшем возбужденном состоянии. Определить вероятность нахождения частицы в интервале l/2, равноудаленном от стенок ямы.

12862
Частица находится в одномерной бесконечно глубокой потенциальной яме шириной L на втором энергетическом уровне Оценить вероятность нахождения частицы в области, ограниченной координатами х₁ = L/4 и x₂ = 5L/8. Построить график зависимости |ψ_n(x)|² для n = 2 и указать рассматриваемый интервал на чертеже.

17251
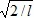
Волновая функция ψ(x) = sin(πx/l) описывает основное состояние частицы в бесконечно глубокой прямоугольной потенциальной яме шириной l. Вычислить вероятность нахождения частицы в малом интервале Δl = 0,01l в средней части ямы

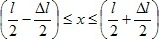
17687
Частица в потенциальном ящике шириной l находится в низшем возбужденном состоянии. Определить вероятность нахождения частицы в интервале l/4, равноудаленном от стенок ящика.

21057
Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 0 < x < l/4 на втором энергетическом уровне.

22096
Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях одномерной потенциальной ямы, ширина которой L, в интервале 0<х<L/4.

23173
Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале Δx = l/4 равноудаленном от стенок одномерной потенциальной ямы шириной l. Поясните смысл полученного результата графически.

23889
Частица находится в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Ширина ямы — l. Состояние частицы описывается главным квантовым числом n. Определить: 1) вероятность нахождения частицы в области "ямы" Δ l = x₂–x₁; 2) точки интервала [х₁, х₂], в которых плотность вероятности существования частицы максимальна и минимальна. n = 1, x₁ = 0,4l, x₂ = 0,9l.