v0054
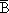
Найти вероятность Р(А) по данной вероятности: P(AB)=0,72, P(A)=0,18.

v0056
Есть три партии деталей. Первая партия содержит 20 стандартных и 10 бракованных деталей, вторая - 15 стандартных и 15 бракованных, третья - 12 стандартных и 18 бракованных деталей. Какая вероятность того, что из наугад выбранной партии наугад взятые 2 детали окажутся стандартными?

v0057
Есть два ящика. В первом ящике размещается 6 стандартных и 4 бракованных детали, второй ящик - пустой. Из первого ящика наугад берут 3 детали и кладут во второй. Какова вероятность взять из второго ящика одну стандартную деталь?

v0058
Три станка-автомата делают однотипные болты, причем первый станок за смену делает 26% всей продукции, второй - 34%, третий - 40%. Доля брака в сделанной продукции первого станка составляет 7%, второго - 2%, третьего - 5%. Наугад взятый болт оказался бракованным. Какая вероятность того, что его изготовил третий станок-автомат.

v0061
Трое рабочих изготовляют однотипные детали. За смену первый рабочий изготовил 200 деталей, второй - в 5 раз меньше, чем первый, а третий - в 2 раза больше, чем второй. Среди деталей, изготовленных первым рабочим, 0,5% бракованных, вторым - 0,8%, третьим - 0,2% бракованных. Все изготовленные детали размещают в одну емкость. Взятая наугад одна деталь оказалась бракованной. Какая вероятность того, что деталь была изготовлена первым или третьим рабочим.

v0062
На складе телевизионного ателье 45% кинескопов, изготовленных заводом №1, 35% - заводом №2, 20% - заводом №3. Вероятность того, что кинескоп не выйдет из строя на протяжении гарантийного срока службы, равна 0,95 для завода №1, 0,98 - для завода №2, 0,88 - для завода №3. Какая вероятность того, что его изготовил завод №2, если взятый наугад кинескоп выдержал гарантийный срок службы?

v0065
На склад поступает продукция, изготовленная на трех фабриках, причем изделия первой фабрики на складе составляют 38%, второй - 42%, третьей - 20%. В продукции первой фабрики брак составляет 7%, второй - 3%, третьей - 1%. Наугад взятое со склада изделие оказалось качественным. Какая вероятность того, что его изготовила третья фабрика?

v0069
Вероятность успеха в любом из 784 независимых испытаний постоянна и равна 0,9. Найти вероятность того, что относительная частота появления успеха отклонится по абсолютной величине от его вероятности не более, чем на 0,08.

v0070
В ящике помещается 12 деталей, изготовленных на заводе №1, 20 деталей - на заводе №2 и 18 деталей - на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и №3, эта вероятность соответственно равна 0,6 и 0,9. Найти вероятность того, что извлеченная наугад деталь окажется отличного качества.

v0071
В первой урне помещается 10 шаров, из них 8 белых. Во второй урне 20 шаров, из них 4 белых. Из каждой урны наугад вытянули по одному шару, а потом из этих двух шаров наугад взят один шар. Найти вероятность того, что взят белый шар.

v0123
Задумано двузначное число, цифры которого различны. Найти вероятность того, что случайно названное двузначное число окажется равным задуманному числу.

v0128
В читальном зале есть 6 учебников по теории вероятностей, из которых 3 в обложке. Библиотекарь наугад взял 2 учебника. Найти вероятность того, что оба будут в обложке.

v0129
В цеху работают 3 женщины и 7 мужчин. За табельными номерами наугад отобрано 3 человека. Найти вероятность того, что все три человека окажутся мужчинами.

v0130
В ящике 5 шаров с номерами от 1 до 5. Наугад вытягивают поочередно 3 шара без возвращения их в ящик. Найти вероятность того, что последовательно появятся шары с номерами 1, 4, 5.

v0131
На складе сохраняется 250 теодолитов. Из них: 202 – технически исправные, 41 – требуют проверки и юстировки, остаток – бракованные. Найти вероятность того, что взятый наугад теодолит можно использовать в работе.

v0132
Вероятность изготовления на автоматическом станке нивелирных рельсов равняется 0,90. Найти вероятность того, что из 10 наугад взятых рельсов 8 окажутся стандартными.

v0144
В первом ящике 8 белых и 6 черных шара, во втором — 6 белых и 5 черных. Из каждого ящика наугад вынимают по одному шару. Чему равна вероятность того, что вынутые шары разного цвета.

v0145
Ящик содержит 12 деталей, среди которых 3 стандартных. Найти вероятность того, что из наугад отобранных 5 деталей окажется более одной стандартной.

v0930
На пяти карточках написано по одной цифре из набора 1,2,3,4,5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой.

v0931
Слово "РАКЕТА", составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробки. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово "КАРЕТА".

v0932
Ящик содержит 12 деталей, среди которых 3 стандартных. Найти вероятность того, что из наугад отобранных 5 деталей окажется более одной стандартной.

v0990
На пяти карточках написано по одной цифре из набора 1,2,3,4,5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой.

v0991
Слово "РАКЕТА", составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробку. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово "КАРЕТА".

v1007
Из полного набора костей домино наугад берутся две кости. Определить вероятность того, что их можно приставить одну к другой.

v1011
В ящике находится 15 теннисных мячей; среди них 9 новых. Для первой игры наугад берутся три мяча. После игры они возвращаются в ящик. Для второй игры также берутся три мяча. Найти вероятность того, что все мячи, взятые для второй игры, были новыми.

v1023
В урне лежат 15 красных, 9 синих и 6 зеленых одинаковых шаров. Наугад берут n = 6 шаров. Какая вероятность, что вынуто: 1 зеленых, 2 синих и 3 красных шаров?

v1025
В лифт 9-этажного дома на первом этаже зашли 6 мужчин. Найти вероятность того, что все выйдут на разных этажах, если каждый может выйти на любом этаже с одинаковой вероятностью.

v1026
Из 20 лотерейных билетов два выигрышных. Найти вероятность того, среди взятых наугад 4 билетов: а) 1 выигрышный; б) по крайней мере один выигрышный.

v1027
9 пассажиров садятся в 3 вагона. Найти вероятность того, что а) в каждый вагон сядут по три пассажира; б) они сядут так:
а) в первый вагон - 3 пассажира;
во второй вагон - 3 пассажира;
в третий вагон - 3 пассажира;
б) в первый вагон - 4 пассажира;
во второй вагон - 3 пассажира;
в третий вагон - 2 пассажира.

v1031
Среди 30 деталей 8 бракованных. Какова вероятность того, что взятые наугад 5 деталей будут без дефекта?

v1034
В урне лежат 7 красных, 4 черных шарика. Какова вероятность того, что из четверых выбранных наугад шариков будет два красных?

v1039
В конверте находятся 100 фотографий. Из конверта наугад выбрали 10 фотографий. Найти вероятность того, среди выбранных находится нужна.

v1043
В партии с 25 автомобилей 5 имеют дефекты. Из этой партии наугад отобрали 3 автомобили. Найти вероятность того, что; а) среди отобранных будет только два автомобиля без дефектов; б) не большее одного автомобиля с дефектом.

v1046
В партии с 25 автомобилей 5 имеют дефекты. Какая вероятность того, что среди трех наугад отобранных автомобилей будет: а) только два автомобиля без дефектов? б) не большее одного автомобиля с дефектом?

v1051
На полке расположен 22 книги, среди которых находится три тома произведений А.С. Пушкина. Их перемешивают и расставляют в произвольном порядке. Найти вероятность того, что три тома произведений А.С. Пушкина будут стоять рядом.

v1052
В мастерских работает 3 станка. За смену первый станок может потребовать наладки с вероятностью 0,15, второй - с вероятностью 0,1, а третий - с вероятностью 0,12. Найти вероятность, того, что за смену хотя бы один станок потребует наладки.

v1055
Завод выпускает 95% деталей стандартными, причем из них 86% - первого сорта. Найти вероятность того, что наугад взятая деталь будет первого сорта.

v1062
Два студента решают одну задачу. Первый может решить эту задачу с вероятностью 0,8, а второй - с вероятностью 0,9. Найдите вероятность того, что: а) оба решат задачу; б) только один из них решит; в) ни один не решит задачу.

v1077
В мастерской работает три станка. На протяжении смены они требуют наладки с вероятностями 0,05; 0,14; 0,3 соответственно. Найти вероятность того, что: а) наладки будут требовать все станки; б) хотя бы один станок.

v1108
Два экономиста заполняют документы, которые составляют в общую папку. Вероятность сделать ошибку для первого равняется 0,1, а для второго - 0,2.Первый заполнил 40 документов, а второй - 60. Найти вероятность того, что наугад взятый из папки документ будет содержать ошибку. Какая вероятность, что этот документ заполнил второй экономист?

v1125
Высший сорт изделий на предприятии в среднем составляет 35%. Наугад берут сто изделий этого предприятия. Найти наивероятнейшее число изделий высшего сорта среди взятых 100.

v1473
Найти вероятность того, что наудачу взятое натуральное число, не превышающее 1000, кратно либо двум, либо пяти.

v1493
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет выстрел из наудачу взятой винтовки.