Изменение внутренней энергии газа совершающего работу

10154
Кислород массой m = 200 г занимает объем V₁ = 100 л и находится под давлением p₁ = 200 кПа. При нагревании газ расширился при постоянном давлении до объема V₂ = 300 л, а затем его давление возросло до р₃ = 500 кПа при неизменном объеме. Найти изменение внутренней энергии δU газа, совершенную газом работу А и теплоту Q, переданную газу. Построить график процесса.

10156
Азот массой m = 0,1 кг был изобарно нагрет от температуры T₁ = 200 К до температуры T₂ = 400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение δU внутренней энергии азота.

10644
Кислород массой m = 2 кг занимает объем V₁ = 1 м³ и находится под давлением p₁ = 0,2 МПа. При нагревании газ расширился при постоянном давлении до объема V₂ = 3 м³, а затем его давление возросло до р₃ = 0,5 МПа при неизменном объеме. Найти изменение внутренней энергии ΔU газа, совершенную газом работу А и теплоту Q, переданную газу. Построить график процесса.

13335
При изобарном нагревании некоторого идеального газа (v = 2 моль) на ΔT = 90 К ему было сообщено количество теплоты 5,25 кДж. Определите: 1) работу, совершаемую газом; 2) изменение внутренней энергии газа; 3) величину γ = с_р/с_v.

13339
Азот массой m = 14 г сжимают изотермически при температуре Т = 300 К от давления р₁ = 100 кПа до давления р₂ = 500 кПа. Определите: 1) изменение внутренней энергии газа; 2) работу сжатия; 3) количество выделившейся теплоты.

13341
Азот массой m = 50 г находится при температуре T₁ = 280 К. В результате изохорного охлаждения его давление уменьшилось в n = 2 раза, а затем в результате изобарного расширения температура газа в конечном состоянии стала равной первоначальной. Определите: 1) работу, совершенную газом; 2) изменение внутренней энергии газа.

13343
При адиабатном расширении кислорода (ν = 2 моль), находящегося при нормальных условиях, его объем увеличился в n = 3 раза. Определите: 1) изменение внутренней энергии газа; 2) работу расширения газа.

50142
При адиабатном процессе над газом совершена работа ΔА = –3·10⁹ Дж. Как изменилась при этом внутренняя энергия газа? Что произойдет с газом — охлаждение или нагревание?

50147
При изохорном процессе газу сообщено 4·10¹⁰ Дж теплоты. Рассчитать изменение внутренней энергии и работу по расширению газа.

50150
Один килограмм углекислого газа CO₂ изобарно нагрет от 268 до 400 К. Определить работу, совершенную над газом при увеличении его объема, и изменение внутренней энергии этого газа.

50297
Кислород занимает объем 2 л при давлении 0,2МПа, а при давлении 1МПа та же масса газа занимает объем 5 л. Определите количество теплоты, сообщенное газу в процессе перехода из первого состояния во второе, изменение внутренней энергии и совершенную газом работу, если процесс происходит: 1) сначала изохорно, затем изобарно; 2) сначала изобарно, затем изохорно. Объясните совпадение и различие ответов.

50399
При изотермическом расширении одного моля водорода была затрачена теплота 4 кДж, при этом объем водорода увеличился в пять раз. При какой температуре протекает процесс? Чему равно изменение внутренней энергии газа и какую работу совершает газ?

50419
При изобарическом сжатии азота была совершена работа, равная 12 кДж. Определить затраченное количество теплоты и изменение внутренней энергии газа.

50421
Газ объемом 2 м³ при изотермическом расширении изменяет давление от 12·10⁵ Па до 2·10⁵ Па. Определить работу расширения, изменение внутренней энергии и подведенную теплоту.

26700
Кислород занимает объем 5 л при давлении 0,2 МПа, а при давлении 1 МПа та же масса газа занимает объем 2 л. Определить количество теплоты, сообщенное газу в процессе перехода из первого состояния во второе, изменение внутренней энергии и совершенную газом работу, если процесс происходил: 1) сначала изохорно, затем изобарно; 2) сначала изобарно, затем изохорно. Объясните совпадение и различие ответов.

11064
Азот, масса которой 28 г, содержится в цилиндре под невесомым подвижным поршнем и занимает объем V₁ при давлении р₁ и температуре t = 27 °С. Затем газ вследствие нагревания медленно расширяется при p₁ = const до объема V₂ и нагревается до температуры Т₂. Для нагрева газа расходуется Q = 10 кДж теплоты. Вычислить работу А расширение газа, изменение его внутренней энергии ΔU, температуру Т₂ и отношение V₂/V₁.

11417
Азот нагревался при постоянном давлении, причем ему было сообщено количество теплоты Q = 21 кДж. Определить работу А, которую совершил при этом газ, и изменение ΔU его внутренней энергии.

15549
Над газом провели некоторый процесс, в ходе которого он отдал 5,2 кДж теплоты. Какую работу совершили над газом, если он перешел из состояния с внутренней энергией 6,2 кДж в состояние с внутренней энергией 4,3 кДж? Ответ выразить в кДж, округлив до десятых.

15700
Над газом провели некоторый процесс, в ходе которого он отдал 5,2 кДж теплоты. Какую работу совершили над газом, если он перешел из состояния с внутренней энергией 6,2 кДж в состояние с внутренней энергией 4,3 кДж? Ответ выразить в кДж, округлив до десятых.

17463
Газ, расширяясь, переходит из одного и того же начального состояния с объемом V₁ в конечное состояние с объемом V₂. а) изобарически; б) адиабатически. Постройте графики этих процессов в координатах P-V. В каком процессе изменение энтропии минимально, а совершаемая работа максимальна?

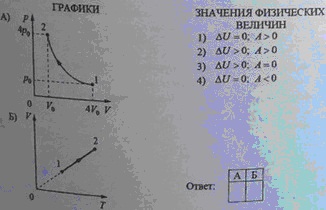
18302
Установите соответствие между графиками процессов, в которых участвует 1 моль идеального газа, и значениями физических величин, характеризующих эти процессы (ΔU — изменение внутренней энергии; A — работа газа). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

19209
Гелий нагревался при постоянном давлении, при этом газу было сообщено 20 кДж теплоты. Определить изменение внутренней энергии газа и совершенную работу.

19734
Некоторая масса азота при давлении 0,1 МПа имела объем 5 л, а при давлении 0,3 МПа имела объем 2 л. Переход от первого состояния ко второму происходил сначала по изохоре, а затем по изобаре. Найти изменение внутренней энергии газа, полученное им количество теплоты и произведенную работу. Построить график процесса в координатах p,V и V,T.

19735
Некоторая масса кислорода при давлении 100 кПа имела объем 10 л, а при давлении 300 кПа - объем 4 л. Переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по изохоре. Определить изменение внутренней энергии газа и произведенную им работу. Построить график этого процесса в координатах p,V и p,Т.

19736
Некоторая масса азота при давлении 0,1 МПа имела объем 5 л, а при давлении 0,5 МПа — объем 2 л. Переход от первого состояния ко второму был сделан в два этапа: сначала по изохоре, затем по изобаре. Определить изменение внутренней энергии газа и произведенную им работу. Построить график процесса в координатах p,V и р,Т.

19738
Масса азота 3 кг занимает объем 2 м³ и находится под давлением 10⁵ Па. Газ нагревают сначала при постоянном объеме, затем при давлении 2·10⁵ Па до объема 4 м³. Построить график процесса в координатах p,V и р,Т, рассчитать изменение внутренней энергии и работу расширения азота.

20051
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — водяной пар
Т₁ = 360 К
Р₁ = 2,4·10⁵ Па
V₁ = 6 л = 6·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20052
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот воздух
Т₁ = 380 К
Р₁ = 2,3·10⁵ Па
V₁ = 5 л = 5·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20053
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот воздух
Т₁ = 380 К
Р₁ = 2,3·10⁵ Па
V₁ = 5 л = 6·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20054
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот гелий
Т₁ = 380 К
Р₁ = 2,2·10⁵ Па
V₁ = 5 л = 6·10^–3 м³
a = 3
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20055
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот кислород
Т₁ = 440 К
Р₁ = 1,2·10⁵ Па
V₁ = 5 л = 6·10^–3 м³
a = 3
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20058
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот кислород
Т₁ = 440 К
Р₁ = 1,2·10⁵ Па
V₁ = 6 л = 6·10^–3 м³
a = 3
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20060
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — углекислый газ
Т₁ = 400 К
Р₁ = 1,3·10⁵ Па
V₁ = 5 л = 5·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20061
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — углекислый газ
Т₁ = 400 К
Р₁ = 1,3·10⁵ Па
V₁ = 6 л = 6·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20062
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот
Т₁ = 450 К
Р₁ = 1,3·10⁵ Па
V₁ = 5 л = 5·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20063
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот
Т₁ = 450 К
Р₁ = 1,3·10⁵ Па
V₁ = 6 л = 6·10^–3 м³
a = 3
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20064
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот воздух
Т₁ = 400 К
Р₁ = 1,2·10⁵ Па
V₁ = 5 л = 5·10^–3 м³
a = 3
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20065
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P₁, V₁, T₁. Объем газа после изотермического расширения V₂ = aV₁, после адиабатического расширения — V₃ = bV₂.

Дано: газ — азот воздух
Т₁ = 400 К
Р₁ = 1,2·10⁵ Па
V₁ = 6 л = 6·10^–3 м³
a = 3
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т₁).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии.

20883
1 кг кислорода сжимается адиабатически, вследствие чего температура газа возрастает от 20°C до 500°С. Определить: а) работу сжатия; б) изменение внутренней энергии газа; в) во сколько раз изменится объем газа?

21324
Гелий массой m при температуре T расширяется в n = 2,5 раза при постоянном давлении за счет притока извне количества теплоты Q. Работа расширения газа равна А, изменение внутренней энергии — ΔU = 6226,2 Дж. Найти m, Q, A.

21439
Один моль двухатомного газа, находящегося при температуре 400 К, расширяется сначала изотермически от объема V₁ до V₂ = 2V₁, а затем адиабатно до объема V₃ = 3V₁. Определить: 1) работу А_1-2 и А_2-3, совершенную газом на участках 1-2 и 2-3, 2) конечную температуру Т₃, 3) изменением ΔU_1-3 внутренней энергии газа на участке 1-3.

21440
Один моль одноатомного газа, находящегося при температуре T₁ = 300 К сжимается сначала изотермически, так, что давление возрастает от p₁ до р₂ = 2p₁, а затем адиабатно до давления р₃ = 4p₁. Определить: 1) работу А_1-2 и А_2-3 на участках 1-2 и 2-3, 2) конечную температуру Т₃, 3) изменение ΔU_1-3 внутренней энергии на участке 1-3.

23029
При изотермическом расширении двухатомного газа, имеющего объем V₁ = 2 м³ давление P₁ = 0,5 МПа, произошло уменьшение давления до P₂ = 0,4 МПа, а затем газ сжали изобарически до первоначального объема. Нарисуйте график этого процесса в координатах Р–V покажите на графике работу газа при этом процессе. Определите работу, совершенную газом, изменение его внутренней энергии и изменение S при этом процессе.

23831
Диета человека массой 70 кг содержит 400 г белка (20,1 МДж/кг), 22 г жиров (39,8 МДж/кг) и 80 г углеводов (16,7 МДж/кг). Каждый день он поднимается на высоту 3 км и совершает перед этим работу, включая работу метаболизма, в четыре раза превышающую механическую работу поднятая своего тела на высоту 3 км. Чему равно изменение внутренней энергии при таком ежедневном процессе?

24361
Идеальный газ совершает цикл а→b→с→d→а, состоящий из процессов, указанных в таблице 9.

Газ	параметры	вид процесса				найти
Газ	параметры	a→b	b→c	c→d	d→a	найти
CO₂	P_c = P₂, P_a = P₁, V_b = V₂	P = const	V = const	T = const	d = a	Q_a→b

Примечание: d = a — процесс отсутствует.

m, г	P₁, МПа	P₂, МПа	P₃, МПа	V₁, л	V₂, л
1	0,2	0,1	0,15	1	2

1) постройте цикл в координатах (Р, V) и Определите для одного из процессов величину, указанную в последнем столбце таблицы 9;
2) для всех участков цикла укажите знак изменения внутренней энергии и Определите получает или отдает газ тепло, совершает газ работу или работа совершается над газом (ответы запишите в таблицу, пояснив ответ расчетами);
3) воспользовавшись результатами решения задачи 1, определите изменение энтропии газа на участке а→b→с цикла (ответы запишите в таблицу, пояснив ответ расчетами);
4) тепловой двигатель работает по циклу, указанному выше для выполненного ранее варианта. Определите его КПД. Каков был бы КПД тепловой машины, работающей по циклу Карно, если бы температура ее нагревателя и холодильника были бы соответственно равны максимальной и минимальной температурам в цикле, описанном в задаче 1 (ответы запишите в таблицу, пояснив ответ расчетами).