10751
Проволочный виток радиусом R = 20 см расположен в плоскости магнитного меридиана. В центре витка установлена небольшая магнитная стрелка, могущая вращаться вокруг вертикальной оси. На какой угол отклонится стрелка, если по витку пустить ток силой I = 12 А? Горизонтальную составляющую индукции земного магнитного поля принять равной В = 20 мкТл.

13662
Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии x = 15 см от его середины. Определите период колебаний стержня, если он совершает малые колебания.

16253
Человек массы m₁ стоит на краю горизонтального однородного диска массы m₂ и радиуса R, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол φ' относительно диска и остановился. В процессе движения скорость человека относительно диска зависела от времени по закону v' (t). Пренебрегая размерами человека, найти: а) угол, на который повернулся диск к моменту остановки человека; б) момент силы относительно оси вращения, с которой человек действовал на диск в процессе движения.

40597
Тонкая прямоугольная пластина может свободно вращаться вокруг горизонтальной оси аa₁, совпадающей с одной из ее коротких сторон. Длинная сторона b = 0,6 м. В точку, находящуюся ниже оси вращения на расстоянии x = 0,5 м, ударяет пуля массы m₁ = 10 г, летевшая горизонтально перпендикулярно пластине со скоростью v = 200 м/с. Масса пластины m₂ = 8 кг, момент инерции относительно заданной оси J = 1/3m₂b². Какую угловую скорость приобретает пластина, если удар абсолютно упругий? При каком значении x в момент удара не возникнет горизонтальная сила реакции оси, действующая на пластину?

24045
Горизонтальная платформа, имеющая форму диска, может свободно вращаться вокруг вертикальной оси симметрии. На краю платформы стоит человек массой m = 60 кг. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку на платформе? Масса платформы равна 240 кг. Момент инерции человека рассчитывать как для материальной точки.

26563
Однородный стержень длиной 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. Стержень приводят в горизонтальное положение и отпускают. Определить угловое ускорение стержня в начальный момент и в момент, когда стержень отклонится на угол 60° от горизонтали. Чему равна линейная скорость конца стержня при прохождении вертикального положения?

26564
Однородный стержень длиной 1 м может свободно вращаться вокруг горизонтальной оси, проходящей на расстоянии 25 см от его конца. Стержень приводят в горизонтальное положение и отпускают. Определить угловое ускорение стержня в начальный момент и в момент, когда стержень отклонится на угол 60° от горизонтали. Чему равны линейные скорости концов стержня при прохождении вертикального положения?

11020
Шар (m₁, r) соединен со стержнем (m₂, l). Система может вращаться вокруг горизонтальной оси. Стержень отклоняют на угол α от вертикального положения и отпускают. Определить момент импульса системы при прохождении стержнем вертикального положения.

11509
Вертикальный цилиндр может свободно вращаться вокруг вертикальной неподвижной оси. Масса цилиндра М, радиус R. В цилиндр попадает горизонтально летящая пуля массой m со скоростью v и моментально застревает в нем. Траектория пули проходит на расстоянии b от оси цилиндра. Найдите угловую скорость цилиндра после удара, если до удара цилиндр покоился.

12656
Кольцо из алюминиевой проволоки сечением S = 2 мм² может свободно вращаться вокруг горизонтальной оси OO'. Вертикально вверх направлено однородное магнитное поле (B = 20 мТл). Определить угол α, на который отклонится плоскость кольца, если по нему пропустить ток I = 5 А. Плотность алюминия ρ = 2,7·10³ кг/м³.

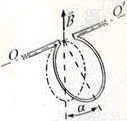
14387
Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m₁ = 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m₂ = 1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?

15616
Однородный стержень массой m, длиной l может свободно вращаться вокруг горизонтальной оси, проходящей на расстоянии l/4 от одного из его концов. Определить период колебаний этого физического маятника.

19670
Однородный тонкий стержень, находящийся на гладкой горизонтальной поверхности, свободно вращается вокруг своего конца с некоторой угловой скоростью ω₀. В некоторый момент ось вытаскивают, и стержень скользит по плоскости, вращаясь. Определить угловую скорость этого вращения.

20009
Однородный сплошной цилиндр массой m₁ = 1 кг может вращаться без трения вокруг оси симметрии. За эту ось он привязан к бруску массой m₂ = 2 кг. К бруску приложена горизонтальная сила, равная 20 Н. Коэффициент трения бруска о плоскость равен 0,1. Определить ускорение цилиндра, если он катиться без проскальзывания.

22109
К потолку лифта, движущемуся вертикально вверх с ускорением а = 1,2 м/с², прикреплен динамометр, к которому подвешен блок, свободно вращающийся вокруг горизонтальной оси. Через блок перекинута нить, к концам которой привязаны грузы массами m₁ = 0,2 кг и m₂ = 0,3 кг. Определить показания динамометра, считая блок невесомым, а нить идеальной. Принять ускорение свободного падения g = 10 м/с². Ответ округлить до десятых.

22626
Однородный стержень длиной 1 м и массой 600 г может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой 7 г, летящая со скоростью 360 м/с перпендикулярно стержню и его оси. С какой угловой скоростью начнет двигаться стержень?

10056
Однородный стержень длиной l = 1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m = 7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол α = 60°. Принять скорость пули v = 360 м/с.

0281g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 30см = 0,3м
H = 28см = 0,28м
d = 26см = 0,26м
V₁ = 0,75V

0282g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 34см = 0,34м
H = 36см = 0,36м
d = 30см = 0,3м
V₁ = 0,75V

0283g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 40см = 0,4м
H = 42см = 0,42м
d = 34см = 0,34м
V₁ = 0,75V

0284g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 56см = 0,56м
H = 50см = 0,5м
d = 46см = 0,46м
V₁ = 0,75V

0285g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 36см = 0,36м
H = 30см = 0,3м
d = 32см = 0,32м
V₁ = 0,75V

0286g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 44см = 0,44м
H = 40см = 0,4м
d = 38см = 0,38м
V₁ = 0,75V

0287g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 52см = 0,52м
H = 52см = 0,52м
d = 44см = 0,44м
V₁ = 0,75V

0288g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 48см = 0,48м
H = 45см = 0,45м
d = 42см = 0,42м
V₁ = 0,75V

0289g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 38см = 0,38м
H = 34см = 0,34м
d = 32см = 0,32м
V₁ = 0,75V

0290g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 32см = 0,32м
H = 26см = 0,26м
d = 28см = 0,28м
V₁ = 0,75V

0314g
Цилиндрический сосуд диаметром D и вершиной Н полностью заполнен водой, температура которой 20°C. Диаметр отверстия равен d. Определить: 1) с какой максимальной частотой можно вращать сосуд вокруг его вертикальной оси, чтобы в сосуде осталось 75% начального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению I-I при его вращении с определенной частотой.
D = 42см = 0,42м
H = 38см = 0,38м
d = 36см = 0,36м
V₁ = 0,75V