скорость точки в момент времени
10008
Материальная точка движется в плоскости ху согласно уравнениям x=A1+B1t+C1t2 и y=A2+B2t+C2t2, где B1=7 м/с, C1=-2 м/с2, B2=-1 м/с, С2=0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t=5 с.
10502
Движения двух материальных точек выражаются уравнениями x1 = A1 + В1t + С1t2 и x2 = A2 + В2t + С2t2 где A1 = 20 м; В1 = 2 м/с; С1 = –4 м/с2; A2 = 2 м; B2 = 2 м/с; С2 = 0,5 м/с2. В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?
10505
Точка движется по прямой согласно уравнению х = At+Bt3, где A = 6 м/с; В = 0,125 м/с3. Определить среднюю скорость <Δs/Δt> точки в интервале времени от t1 = 2 с до t2 = 6 с.
10506
Две материальные точки движутся согласно уравнениям х1 = А1+В1t+С1t2 и x2 = А2+C2t2, где A1 = 10 м; В1 = 32 м/с; С1 = –3 м/с2; A2 = 5 м; С2 = 5 м/с2. В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент?
40004
Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид х = A+Bt+Сt3, где А = 4 м, В = 2 м/с, С = –0,5 м/с3. Для момента времени t1 = 2 с Определить: 1) координату x1 точки; 2) мгновенную скорость v1; 3) мгновенное ускорение а1.
40141
Скорость реактивного самолета на некотором участке меняется с расстоянием по закону v = D + Bs. Найти работу за промежуток времени (t1,t2), если масса самолета m. В момент времени t1 скорость равна v1.
40472
Движение двух материальных точек выражается уравнениями x1 = 20 + 2t – 4t2 и x2 = A + Bt + Ct2. В момент времени t скорость этих точек одинаковы. Чему равны скорости и ускорения точек в этот момент.
40548
Материальная точка, совершающая гармонические колебания, в некоторый момент времени имеет смещение, скорость и ускорение, равные соответственно 7 см, 1 см/с, –9 см/с2. Определить фазу колебания в рассматриваемый момент времени. Учесть, что начальная фаза и начальное смещение материальной точки равны нулю. Ответ дать в градусах.
40564
Материальная точка начинает двигаться по окружности с угловым ускорением ε = k∙t, где k = 4 рад/с3. Определить угловую скорость точки в момент времени t1 = 2 c.
40635
По прямой линии движутся две материальные точки согласно уравнениям: х1 = А1 + В1t + С1t2 и x2 = А2 + В2t + С2t2, де А1 = 10 м; В1 = 1 м/с; С1 = -2 м/с2; А2 = 3 м; В2 = 2 м/с; С2 = 0,2 м/с2. В какой момент времени скорости этих точек будут одинаковыми? Найти ускорение а1 и а2 этих точек в момент t = 3 с.
40721
Начальная фаза колебаний точки равна π/3. Период колебаний Т = 0,06с. Определить ближайшие моменты времени, в которые скорость и ускорение в два раза меньше амплитудных значений.
40635
По прямой линии движутся две материальные точки согласно уравнениям: х1 = А1 + В1t + С1t2 и x2 = А2 + В2t + С2t2, де А1 = 10 м; В1 = 1 м/с; С1 = -2 м/с2; А2 = 3 м; В2 = 2 м/с; С2 = 0,2 м/с2. В какой момент времени скорости этих точек будут одинаковыми? Найти ускорение а1 и а2 этих точек в момент t = 3 с.
26598На материальную точку массой 2 кг действует сила постоянного направления, значение которой изменяется по закону F = 6t
2. Определить скорость этой точки в момент времени t = 2 с, если начальная скорость точки v
0 = 2 м/с.

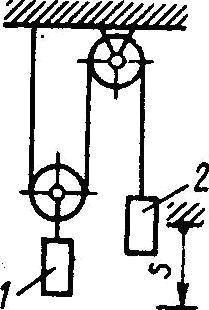
26616Определить скорость груза 2 в момент времени, когда он опустился вниз на расстояние s = 4 м, если массы грузов m
1 = 2 кг, m
2 = 4 кг. Система тел вначале находилась в покое.
26711
Проекции ускорения точки во время движения определяются выражениями ax = 0,8t (м/с2), ay = 0,8 м/с2. Найти касательное ускорение в момент времени t = 2 с, если при t0 = 0 скорость точки v0 = 0.
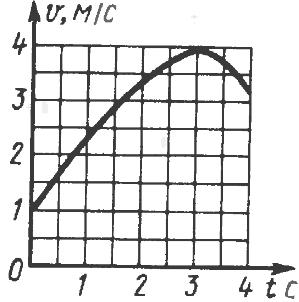
26712Дан график скорости v = v(t) движения точки по окружности радиуса 6 м. Определить нормальное ускорение точки в момент времени t = 3 с.
11396
По прямой линии движутся две материальные точки согласно уравнениям: х1 = 10 + t + 2t2 и x2 = 3 + 2t + 0,2t2. В какой момент времени скорости этих точек одинаковы?
12956
Точка движется по прямой согласно уравнению x = At – Bt3 – С, где А = 4 м/с, В = 3 м/с3, С = 1 м. Найти координаты х точки в моменты времени, когда скорость v равна нулю.
13302
Кинематические уравнения движения двух материальных точек имеют вид х1 = А1+B1t+С1t2 и х2 = А2+В2t+C2t2, где (пропущено в книге: B1 = B2), C1 = –2 м/c2, С2 = 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента.
15168
Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 2 м, В = 1 м/с, С = –0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
15213
Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct3, где А = 2 м, В = –1 м/с, С = –0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 10 с.
15221
Уравнение движения материальной точки вдоль оси имеет вид х = А + Bt + Ct2, где А = 2 м, В = 1 м/с, С = –0,5 м/с2. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
15233
Уравнение движения материальной точки вдоль оси имеет вид х = А – Bt – Ct3, где А = 2 м, В = –1 м/с, С = 0,5 м/с3. Найти координату х, скорость vx и ускорение ах в момент времени τ = 2 с.
15934
Уравнение движения точки имеет вид x = –0,4t2. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 20 c, Δt = 2,0 c); 6) указать характер движения точки.
15935
Уравнение движения точки имеет вид x = 2+5t. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 50 c, Δt = 5,0 c); 6) указать характер движения точки.
15936
Уравнение движения точки имеет вид x = 150–10t. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 40 c, Δt = 4,0 c); 6) указать характер движения точки.
15937
Уравнение движения точки имеет вид x = 400–0,6t. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 100 c, Δt = 10,0 c); 6) указать характер движения точки.
15938
Уравнение движения точки имеет вид x = 10t+0,4t2. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 20 c, Δt = 2,0 c); 6) указать характер движения точки.
15939
Уравнение движения точки имеет вид x = 2t–t2. По уравнению Определить: 1) координату х0 точки в начальный момент времени; 2) начальную скорость v0 точки; 3) ускорение а точки; 4) написать формулу зависимости скорости от времени v = f(t); 5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 < t < τ с шагом Δt (τ = 15 c, Δt = 1,5 c); 6) указать характер движения точки.
16072
Материальная точка на плоскости совершает движение, которое задается кинематическими уравнениями: х = A∙cos(ω∙t); у = B∙cos(ω∙t + φ0), где х и у — координаты точки в момент времени t, А = 4 м, В = 8 м, φ0 = π, ω = π рад/с. Определить траекторию точки и скорость точки в момент времени t1 = 1 с.
17200
Движение точки задано уравнениями x = A1sinωt и y = A2sinω(t+τ), где А1 = 10 см, А2 = 5 см, ω = 2 рад/с, τ = π/4 с. Найти уравнение траектории и скорости точки в момент времени t = 0,5 с.
17238
Радиус-вектор точки изменяется со временем по закону: r = 2t2i + tj + k. Найти скорость v и ускорение w точки, модуль скорости v в момент t = 2 с, приближенное значение пути S, пройденного точкой за 10-ю секунду движения.
18972
Уравнение движения материальной точки по прямой имеет вид x = A + Bt + Ct2, где А = 4 м, В = 2 м/с, С = –0,5 м/с2. Для момента времени t1 = 2 секунды Определить координату точки и мгновенное ускорение. Найти путь, пройденный точкой, и среднюю скорость за промежуток времени от t1 = 2c до t2 = 6c.
19146
Диск массой 300 г катится с линейной скоростью 3 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатится. Мгновенная ось, относительно которой он вращается в данный момент времени, есть точка соприкосновения диска с плоскостью.
19177
Обруч массой 1 кг катится с линейной скоростью 5 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатывается. Мгновенная ось, относительно которой обруч вращается в данный момент времени, есть точка соприкосновения обруча с плоскостью.
19178
Цилиндр массой 1 кг движется с линейной скоростью 3 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатится. Мгновенная ось, относительно которой цилиндр вращается в данный момент времени, есть точка соприкосновения цилиндра с плоскостью.
19314
При незатухающих гармонических колебаниях точки ее максимальная скорость равна 0,1 м/с, а максимальное ускорение равно 1 м/с2. Написать уравнение колебаний, считая, что в начальный момент времени смещение максимально.
19502
Две материальные точки движутся вдоль одной прямой с ускорениями a1 = A1+B1t, a2 = A2+B2t, где A1 = 4 м/c2, B1 = 3 м/с3, A2 = 12 м/с2, B2 = –1 м/с3. Начальные скорости этих точек были равны, соответственно, 8 м/с и 12,5 м/с. В какой момент времени t скорости точек будут одинаковы?
15245
Движение материальной точки описано уравнением x = 5 – 6t + 2t2. Найти среднюю скорость за промежуток времени от 1 до 2 с. Найти скорость и ускорение точки в начальный и конечный моменты времени.
20113
Уравнение движения точки по прямой имеет вид: х = 2 + 6t – t2 (м). Найти: 1) путь и перемещение точки за промежуток времени от t1 = 2 с до t2 = 4 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 2 с.
20123
Уравнение движения точки по прямой имеет вид: х = –1–3t2+2t3 (м). Найти: 1) путь и перемещение точки за промежуток времени от t1 = 0 с до t2 = 2 с; 2) среднюю скорость и среднее ускорение точки за этот промежуток; 3) скорость и ускорение точки в момент времени t = 1 с.
20161
Частица движется так, что ее скорость изменяется со временем по закону v(t) = 3t2∙i + t∙j – 2∙k (м/с), где t - время в секундах. В начальный момент времени t0 = 0 частица находилась в точке с координатами (0; 1 м; 0). Найти: 1) зависимость от времени модуля скорости частицы; 2) зависимости от времени вектора ускорения и модуля ускорения; 3) кинематический закон движения частицы; 4) радиус-вектор в момент времени t1 = 1,0 с; 5) модуль перемещения частицы за время Δt = t1 – t0.
20162
Частица движется так, что ее скорость изменяется со временем по закону v(t) = t3∙i + 2∙j – t2∙k (м/с), где t — время в секундах. В начальный момент времени t0 = 0 частица находилась в точке с координатами (0; 0; 1 м). Найти: 1) зависимость от времени модуля скорости частицы; 2) зависимости от времени вектора ускорения и модуля ускорения; 3) кинематический закон движения частицы; 4) радиус-вектор в момент времени t1 = 1,0 с; 5) модуль перемещения частицы за время Δt = t1 – t0.
21417
Материальная точка совершает прямолинейное движение. Закон движения имеет вид x(t) = Bt + Ct2 + Dt3, В = 2 м/с, С = 1 м/с2, D = –0,3 м/с3. Найти зависимость скорости и ускорения точки от времени. Определить координату х, скорость v и ускорение а, которые будет иметь точка в момент времени t = 3 с . Какой путь пройдет точка за это время? Построить графики зависимости x(t), v(t) и a(t) в интервале от t = 0 с до t = 5 с.
21462
Определить смещение точки М через 0,3 с после начала колебаний. Расстояние точки до источника колебаний 80 м, скорость волны 320 м/с, амплитуда волны ξm = 2,5 мм. Период колебаний источника 0,2 с, смещение источника колебаний в начальный момент времени равно половине амплитуды. Колебания источника происходят по закону косинуса.
21480
Зависимость координаты материальной точки от времени выражается уравнением: x(t) = 1,5t2–0,25t3, м. Вычислите: 1) зависимость скорости и ускорения от времени; 2) скорость и ускорение в момент времени t = 1 c; 3) максимальную скорость точки; 4) перемещение через 3 с от начала движения; 5) постройте графики зависимостей: x = f(t), v = f(t), a = f(t); 6) назовите характер движения тела.
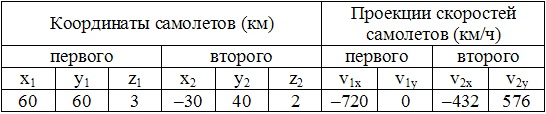
26498У диспетчера аэропорта к моменту начала дежурства (20 ч 00 мин 00 с) имеется информация о движении двух самолетов, приведенная в таблице 1.1. Используемая в ней система координат имеет начало в точке размещения диспетчера, ось 0х направлена на восток, а ось 0у - на север.
1. Отметьте на координатной плоскости 0xy положения воздушных судов и направления их полетов.
2. Запишите законы движения самолетов.
3. Определите время вылета одного из самолетов из аэропорта.
4. Определите минимальное расстояние, на которое сближаются самолеты, и время, когда произойдет сближение.
5. Найдите модуль скорости первого самолета в системе отсчета, движущейся вместе со вторым самолетом.
Скорости самолетов считать неизменными. Размерами аэропорта пренебречь.
25360
Движение материальной точки задано уравнением x = At+Bt2, где А = 4 м/с, В = –0,05 м/с2. Определить момент времени, в который скорость точки равна нулю. Найти путь, пройденный точкой, координату и ускорение точки в этот момент. Найти среднюю скорость точки за промежуток времени с момента начала движения до момента равенства ее скорости нулю.
25640
Движение материальной точки задано уравнением r(t) = i(A+Bt2)+jCt, где A = 10 м, В = –5 м/с2, С = 10 м/с. Начертить траекторию точки. Найти выражения v(t) и a(t). Для момента времени t = 1 с вычислить: 1) модуль скорости |v| ; 2) модуль ускорения |а|; 3) модуль тангенциального ускорения |аτ|; 4) модуль нормального ускорения |аn|.


