60587
Определить полный заряд, который равномерно распределен по тонкому стержню длиной 40 см, если создаваемая им напряженность электрического поля в точке, лежащей на продолжении стержня на расстоянии 20 см от ближайшего конца, равна 60 кВ/м.

11755
Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями σ₁ = 2 нКл/м² и σ₂ = –5 нКл/м². Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.

11733
Определить напряженность Е электрического поля, создаваемого точечным зарядом Q = 10 нКл на расстоянии r = 10 см от него. Диэлектрик — масло.

11676
Две прямоугольные одинаковые параллельные пластины, длины сторон которых а = 10 см и b = 15 см, расположены на малом (по сравнению с линейными размерами пластин); расстоянии друг от друга. На одной из пластин равномерно распределен заряд Q₁ = 50 нКл, на другой — заряд Q₂ = 150 нКл. Определить напряженность E электрического поля между пластинами.

12073
На проводящей тонкой сфере радиусом R распределен положительный заряд Q = 2q. В центре сферы находится точечный положительный заряд q. Найти напряженность Е(r) электрического поля как функцию расстояния r от центра сферы. Построить примерный график зависимости Е(r).

12214
Две длинные прямые параллельные нити находятся на расстоянии d = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями τ₁ = –5 нКл/см и τ₂ = 10 нКл/см. Определить напряженность электрического поля Е в точке, удаленной от первой нити на расстояние r₁ = 3 см и от второй на расстояние r₂ = 4 см.

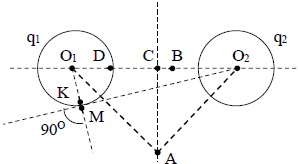
13219
На рисунке 14.1. показаны две тонкостенные сферы, имеющие радиусы 0,2 м и заряды 16·10^–6 Кл, равномерно распределенные по поверхности. Расстояние между центрами сфер 80 см. Точка C лежит в середине между сферами, точка D внутри сферы в непосредственной близости от стенки. Найти разность потенциалов электрического поля между точками C и D и напряженность в точке D.

13265
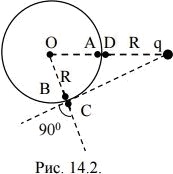
Сферическая тонкая оболочка с радиусом R = 5 см имеет равномерно распределенный по поверхности положительный заряд с плотностью σ = 8 мкКл/м². На расстоянии R от ее поверхности находится точечный заряд q. Какова величина и знак этого заряда, если известно, что потенциал электрического поля в центре сферы равен 0? Какова напряженность поля в точке D, находящейся в непосредственной близости от сферы, как показано на рис. 14.2?

13386
При значении напряженности электрического поля E₀ = 3·10⁶ (В/м) воздух перестает быть надежным изолятором и в нем происходят искровые разряды. Каким минимальным может быть радиус шара R, чтобы он мог удерживать заряд Q = 1 Кл (в воздухе).

13497
На рисунке 14.2 изображена отрицательно заряженная тонкостенная сфера радиусом R = 20 см, имеющая равномерно распределенный заряд с поверхностной плотностью σ = –0,2 мкКл/м², и точечный заряд q = 100 нКл, находящийся на расстоянии R от поверхности сферы. Рассчитать напряженность и потенциал электрического поля в точках В и С, которые находятся в непосредственной близости от стенки сферы соответственно внутри и вне сферы, как показано на рис. 14.2.

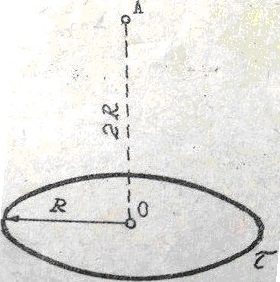
14606
По тонкому кольцу радиуса R = 20 см равномерно распределен с линейной плотностью τ = –0,1 мкКл/м заряд. Определить: 1) напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии 2R от его центра, 2) силу F, действующую на точечный заряд q = 5 нКл, помещенный в точку А.

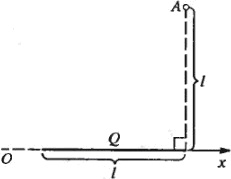
14760
По тонкому стержню длиной l = 20 см равномерно распределен заряд Q = 50 нКл. Определить в точке A (рис. 14.14) напряженность Е электрического поля по модулю и направлению (угол β с осью Ох).

16456
Электрический заряд Q равномерно распределен по тонкому кольцу радиуса R. Найдите напряженность электрического поля, создаваемого этим зарядом в точке, лежащей на оси кольца на расстоянии х от его центра.

17350
В комнату влетела шаровая молния радиуса R = 3 см и объемной плотностью заряда ρ = 5·10^–6 Кл/м³. Чему равен поток вектора напряженности электрического поля N, выходящий за пределы комнаты.

17354
Две бесконечно длинные параллельные нити находятся на расстоянии a = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями τ₁ = –5·10^–9 Кл/м и τ₂ = +10·10^–9 Кл/м. Определить напряженность электрического поля в точке, удаленной от первой нити на расстоянии b = 3 см и от второй — c = 4 см.

19297
Длинный прямой провод, расположенный в вакууме, имеет заряд равномерно распределенный по длине. Линейная плотность заряда τ = 10^–9 Кл/м. Определить напряженность Е электрического поля на расстоянии 1,5 м от провода в средней его части.

20841
Вычислить напряженность электрического поля в точке, расположенной в центре полукольца радиуса R = 0,05 см, если по этому полукольцу равномерно распределен заряд Q = 3·10^–7 Кл.

21465
Из кремния с собственной проводимостью изготовлен цилиндрический образец диаметром 3 мм и длиной 15 мм. Найдите силу тока в образце при температуре 25°С и напряженности электрического поля 3,5 кВ/м. Подвижности носителей зарядов: электронов μ_n = 0,13 м²/(В·с), дырок μ_p = 0,05 м²/(В·с). Ширина запрещенной зоны кремния 1,1 эВ.

21949
Заряд 5,2 мкКл, находящийся на плоскости в точке с координатами (4,4; 3,6) см, создает в точке (7,6; 7,8) см напряженность Е₁, а в точке (-2,3; -2,2) см напряженность Е₂. Найти отношение Е₂/Е₁.

23421
Горизонтально расположенная, неподвижная, положительно заряженная диэлектрическая пластина создает электрическое поле. На нее с высоты 0,10 м начинает падать шарик массой 0,02 кг, имеющий заряд 10,00 мкКл. При абсолютно неупругом ударе шарик передает пластине импульс 0,03 кг·м/с. Какова напряженность электрического поля пластины? Начальная скорость шарика равна нулю.

24606
Заряд 0,5 нКл равномерно распределен по поверхности полого металлического шарика радиусом 2,5 см. Найти потенциал электрического поля в центре, на поверхности шарика и на расстоянии 5 см от центра. Построить график зависимости модуля вектора напряженности поля и потенциала от расстояния до центра шарика.

24758
Заряд равномерно распределен с объемной плотностью ρ = 12 мкКл/м³ в шаровом слое с внутренним радиусом R₁ = 24,0 см и внешним R₂. В точках на расстоянии r = 370,0 см от центра напряженность электрического поля равна Е, а потенциал φ = 1,35 кВ. Определите неизвестную величину R₂.

24760
Заряд равномерно распределен с объемной плотностью ρ = 200 мкКл/м³ в шаровом слое с внутренним радиусом R₁ = 0,8 см и внешним R₂ = 4,9 см. В точках на расстоянии r от центра напряженность электрического поля равна Е = 0,15 кВ/см, а потенциал φ. Определите неизвестную величину r.

24761
Заряд равномерно распределен с объемной плотностью ρ = 50 мкКл/м³ в шаровом слое с внутренним радиусом R₁ = 1,7 см и внешним R₂ = 2,4 см. В точках на расстоянии r = 1,4 см от центра напряженность электрического поля равна Е, а потенциал φ. Определите неизвестную величину φ.

24762
Заряд равномерно распределен с объемной плотностью ρ в шаровом слое с внутренним радиусом R₁ = 2,5 см и внешним R₂ = 3,2 см. В точках на расстоянии r = 2,8 см от центра напряженность электрического поля равна Е, а потенциал φ = 13,0 кВ. Определите неизвестную величину E.

24792
Электрическое поле создается в вакууме зарядом, распределенным по бесконечному цилиндру с объемной плотностью ρ(r), где r – расстояние от оси цилиндра.
1. С помощью теоремы Гаусса вывести формулы зависимостей E(r) напряженности поля системы от расстояния r во всех областях пространства;
2. По полученным выражениям E(r) вывести формулы зависимостей потенциала φ(r) электрического поля системы от расстояния r во всех областях пространства;
3. Записать числовые выражения зависимостей E_r(r) и φ(r) и рассчитать их значение с заданным шагом в заданном диапазоне расстояний r; результаты свести в таблицу;
4. По данным таблицы значений построить в масштабе графики E_r(r) и φ(r).
Нулевой уровень потенциала – на поверхности цилиндра (φ(R)= 0).
n = 1/2, ρ = ρ₀n·r/R, ρ₀ = 0,5 мкКл/м³; R = 5 см.

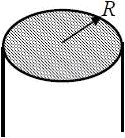
24793
Электрическое поле создается в вакууме зарядом, распределенным по шару с объемной плотностью ρ(r), где r – расстояние от центра шара.
1. С помощью теоремы Гаусса вывести формулы зависимостей E(r) напряженности поля системы от расстояния r во всех областях пространства;
2. По полученным выражениям E(r) вывести формулы зависимостей потенциала φ(r) электрического поля системы от расстояния r во всех областях пространства;
3. Записать числовые выражения зависимостей E_r(r) и φ(r) и рассчитать их значение с заданным шагом в заданном диапазоне расстояний r; результаты свести в таблицу;
4. По данным таблицы значений построить в масштабе графики E_r(r) и φ(r).
Нулевой уровень потенциала – на бесконечности (φ(∞)=0).

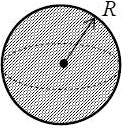
n = 3/2,
ρ = ρ₀n·r/R,
ρ₀ = 0,5 мкКл/м³ = 5·10^–7 Кл/м³,
R = 5 см = 0,05 м

10196
Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью τ = 0,5 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси стержня на расстоянии а = 20 см от его начала.

10200
По тонкому кольцу равномерно распределен заряд Q = 10 нКл с линейной плотностью τ = 0,01 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.