10202
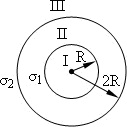
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = 4σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 30 нКл/м², r = 1,5R; 3) построить график E(r).

10203
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = σ, σ₂ = –σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 0,1 мкКл/м², r = 3R; 3) построить график E(r).

10204
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –4σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 50 нКл/м², r = 1,5R; 3) построить график E(r).

10205
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –2σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 0,1 мкКл/м², r = 3R; 3) построить график E(r).

60148
Две концентрические сферы с радиусами 2 см и 4 см имеют заряды 10^–8 Кл и 2·10^–8 Кл. Заряды распределены равномерно. Какую работу совершают силы электрического поля при перемещении точечного заряда 10^–10 Кл из точки, расположенной в 3 см от центра сфер, в точку, расположенную в 6 см от центра сфер?

60402
Радиусы двух проводящих концентрических сфер 31 см и 347 см. На каждой сфере равномерно распределен заряд +487 нКл. Найти разность потенциалов между сферами.

10203
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = σ, σ₂ = –σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 0,1 мкКл/м², r = 3R; 3) построить график E(r).

10204
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –4σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 50 нКл/м², r = 1,5R; 3) построить график E(r).

10205
На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –2σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ = 0,1 мкКл/м², r = 3R; 3) построить график E(r).

12367
На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = –120 нКл/м² и σ₂ = 30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найти зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от центра на расстояние r = 1,5R, и указать направление вектора Е. Построить график зависимости Е(r).

12368
На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = 120 нКл/м² и σ₂ = 30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найти зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от центра на расстояние r = 1,5R, и указать направление вектора Е. Построить график зависимости Е(r).

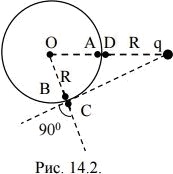
13236
Сферическая поверхность радиусом R = 0,1 м несет равномерно распределенный по ней заряд с поверхностной плотностью σ = 2·10^–7 Кл/м². Вне сферы на расстоянии R от ее поверхности находится точечный заряд q = 4·10^–8 Кл (см. рис. 14.2.). Найти напряженность и потенциал электрического поля в центре сферы.

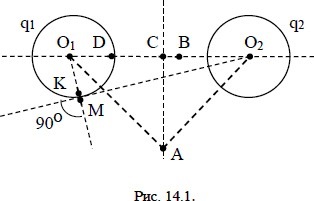
13626
Сферы, изображенные на рис 14.1, имеют радиусы по 0,05 м и заряды q₁ = -46 мкКл и q₂ = 46 мкКл, которые равномерно распределены по их поверхностям. Расстояние между центрами сфер 20 см. Рассчитать напряженность и потенциал электрического поля в точке D, которая находится внутри отрицательно заряженной сферы в непосредственной близости от ее стенки.

14608
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ и σ₂. Используя теорему Гаусса, определить напряженность электрического поля в зависимости от расстояния до оси r. Принять σ₁ = –σ, σ₂ = –2σ, где σ = 10 нКл/м². Радиусы сфер R₁ = R и R₂ = 5R, где R = 10 см. Построить график зависимости напряженности E(r).

15284
Объемный заряд с плотностью 2 нКл/м³ равномерно распределен между двумя концентрическими сферическими поверхностями, причем радиус внутренней поверхности 10 см, а наружной — 50 см. Найдите напряженность поля в точках, отстоящих от центра сфер на расстояниях r₁ = 3 см и r₂ = 56 см.

15713
На двух концентрических сферах равномерно распределенный заряд с поверхностными плотностями σ₁ = 3σ и σ₂ = –σ, где σ = 10 нКл/м². Радиусы сфер R и 2R, где R = 10 см. Определить напряженность электрического поля в зависимости от расстояния до оси r. Найти зависимость E(r), вычислить E(R₁), E(R₂), если R₁ = 1,5R, R₂ = 3R. Построить график зависимости напряженности Е(r).

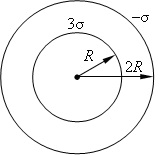
19199
На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями, равными σ₁ и σ₂. Найти зависимость напряженности E электрического поля от r, где r — расстояние от центра сфер. Принять σ₁ = –2σ, σ₂ = σ. Построить график зависимости Е(r).

20554
Две металлические концентрические сферы радиусами 15 и 30 см расположены в воздухе. На внутренней сфере распределен заряд –2·10^–8 Кл, а потенциал внешней сферы равен 450 В. Вычислить напряженность и потенциал в точках, удаленных от центра сфер на 10 и 20 см.

20869
По сфере радиуса R = 10 см равномерно распределен заряд Q = 10^–8 Кл. Сфера вращается с частотой f = 10 1/c относительно оси, проходящей через центр сферы. Найти магнитный момент кругового тока, создаваемого вращающейся сферой.

21620
На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями соответственно σ₁ и σ₂. Используя теорему Гаусса, определить модуль и направление напряженности электрического поля в точке, удаленной от центра сфер на расстояние r. Принять σ₁ = –8σ, σ₂ = σ, r = 1,7R.

21784
Две концентрические сферы радиусами R и 2R равномерно заряжены зарядами q₁ и q₂. Найти напряженности E₁, Е₂, и Е₃ поля в точках, отстоящих от центра сфер на расстояния r₁, r₂ и r₃ соответственно (ε = 1), если r₁ < R < r₂ < 2R < r₃.

22814
Две концентрические сферы несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ и σ₂. Используя теорему Гаусса Определить напряженность электрического поля в зависимости от расстояния до центра сфер r. Принять σ₁ = σ, σ₂ = –σ, где σ = 10 нКл/м². Радиусы сфер R₁ = R и R₂ = 3R, где R = 10 см. Построить график зависимости напряженности Е(r).

22815
Две концентрические сферы несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ и σ₂. Используя теорему Гаусса Определить напряженность электрического поля в зависимости от расстояния до центра сфер г. Принять σ₁ = σ, σ₂ = –4σ, где σ = 50 нКл/м². Радиусы сфер R₁ = R и R₂ = 2R, где R = 10 см. Построить график зависимости напряженности Е(r).

24709
Две концентрические сферы несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ и σ₂. Используя теорему Гаусса Определить напряженность электрического поля в зависимости от расстояния до центра сфер r. Принять σ₁ = –σ, σ₂ = 2σ, где σ = 25 нКл/м². Радиусы сфер R₁ = R и R₂ = 1,5R, где R = 10 см. Построить график зависимости напряженности Е(r).

24829
По поверхности тонкостенной сферы радиуса R равномерно распределен заряд q. Определить напряженность поля Е как функцию расстояния r от центра сферы. Зависимость Е(r) изобразить графически.