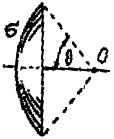10209
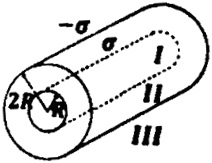
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –2σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 50 нКл/м², r = 1,5R; 3) построить график E(r).

10210
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = σ, σ₂ = –σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 60 нКл/м², r = 3R; 3) построить график E(r).

10211
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –σ, σ₂ = 4σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 30 нКл/м², r = 4R; 3) построить график E(r).

10209
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –2σ, σ₂ = σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 50 нКл/м², r = 1,5R; 3) построить график E(r).

10210
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского—Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = σ, σ₂ = –σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 60 нКл/м², r = 3R; 3) построить график E(r).

10211
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂. Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ₁ = –σ, σ₂ = 4σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 30 нКл/м², r = 4R; 3) построить график E(r).

11173
Две бесконечные пластины расположены параллельно друг другу и несут равномерно распределенные по площади заряды с поверхностными плотностями 10^–3 мкКл/м² и 2·10^–3 мкКл/м². Используя теорему Гаусса, определите напряженность поля: 1) между пластинами, 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.

12131
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ и σ₂. Используя теорему Гаусса Определить напряженность электрического поля в зависимости от расстояния до оси r. Принять σ₁ = σ, σ₂ = -σ, где σ = 10 нКл/м². Радиусы цилиндров R₁ = R и R₂ = 2R, где R = 10 см. Построить график зависимости напряженности Е(r).

12147
На бесконечном толстостенном цилиндре диаметром 10 см равномерно распределен заряд с поверхностной плотностью 10 мкКл/м². Определить (в кВ/см) напряженность поля в точке, отстоящей от поверхности цилиндра на расстоянии 5 см.

13779
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ и σ₂ (см. рис.). Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость E(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять σ₁ = 3σ, σ₂ = σ, 2) вычислить напряженность E в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ = 10 нКл/м²; r = 2R; 3) построить график E(r).

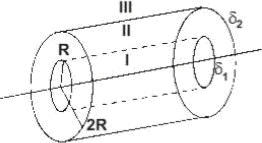
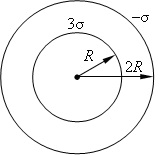
15715
Два коаксиальных цилиндра несут на себе равномерно распределенный заряд с поверхностными плотностями σ₁ = 3σ и σ₂ = –σ, где σ = 10 нКл/м². Определить напряженность электрического поля в зависимости от расстояния до оси r. Радиусы цилиндров R и 2R, где R = 10 см. Найти зависимость E(r), вычислить E(R₁), E(R₂), если R₁ = 1,5R, R₂ = 3R. Построить график зависимости напряженности Е(r).

15915
По поверхности сферического сегмента равномерно распределен электрический заряд с поверхностной плотностью σ = 60 нКл/м². Определить в точке О, совпадающей с центром сферы напряженность Е электрического поля. Угол θ = π/4.

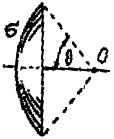
15916
По поверхности сферического сегмента равномерно распределен электрический заряд с поверхностной плотностью σ = 60 нКл/м². Определить в точке О, совпадающей с центром сферы: 1) напряженность Е электрического поля; 2) силу F, действующую на точечный заряд q = 20 нКл. Угол θ = π/4.

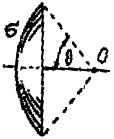
16443
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = –120 нКл/м² и σ₂ = 60 нКл/м². Используя теорему Гаусса, найти зависимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r = 1,5R. Построить график зависимости Е(r).

17129
Непроводящее тонкое плоское кольцо с внутренним радиусом R₁ = 6 см и внешним R₂ = 12 см, равномерно заряженное с одной стороны с поверхностной плотностью заряда σ = 15 мкКл/м², вращается вокруг своей оси с угловой скоростью ω = 60 рад/с.
Определить индукцию В магнитного поля в центре кольца.
Полагая общий заряд на кольце сохраняющимся и равномерно распределенным, построить график зависимости индукции В от радиуса R₂ кольца в пределах 7 < R₂ < 12 см с шагом ΔR₂ = 1 см.

17345
Заряд равномерно распределен по поверхности диска, радиуса R = 10 см. Поверхностная плотность заряда диска равна σ = 10^–9 Кл/м². Найти напряженность электрического поля на оси диска на расстоянии S = 5 см от его центра.

17353
На бесконечно длинном тонкостенном цилиндре диаметром D = 20 см равномерно распределен заряд с поверхностной плотностью σ = 4·10^–6 Кл/м². Определить напряженность электрического поля в точке, отстоящей от оси цилиндра на расстоянии S = 40 см.

17419
На бесконечном тонкостенном цилиндре диаметром d = 10 см равномерно распределен заряд с поверхностной плотностью σ = 2 мкКл/м². Определить напряженность поля в точке, отстоящей от поверхности цилиндра на расстоянии 12 см.

17420
На бесконечном тонкостенном цилиндре диаметром d = 10 см равномерно распределен заряд с поверхностной плотностью σ = 1 мкКл/м². Определить напряженность поля в точке, отстоящей от поверхности цилиндра на a = 5 см.

18152
Полусфера несет заряд, равномерно распределенный с поверхностной плотностью σ = 1 нКл/м². Найти напряженность Е электрического поля в геометрическом центре полусферы.

19299
Найти потенциал φ и напряженность поля Е в центре полусферы радиуса R, заряженной равномерно с поверхностной плотностью заряда σ.

19380
По пластине длиной L = 0,5 м и шириной S = 0,2 м равномерно распределен заряд с поверхностной плотностью σ = 10^–7 Кл/м². Пластина равномерно вращается с частотой f = 20 1/с относительно оси, проходящей через край пластины, параллельно стороне. Определить магнитный момент кругового тока, вызванного вращением пластины вокруг заданной оси.

20842
По тонкому кольцу с внешним и внутренним радиусами (R₁ = 5 см, R₂ = 10 см) равномерно распределен заряд с поверхностной плотностью σ = 10^–9 Кл/м². Вычислить напряженность электрического поля в точке, лежащей на оси кольца, на расстоянии а = 10 см от его центра.

22974
По поверхности шара радиусом 5,00 мм равномерно распределен заряд с поверхностной плотностью 5,00 мкКл/м². Шар находится в вершине прямого угла равнобедренного треугольника с длиной катета 40,0 мм. В двух других вершинах находятся точечные заряды 2,00 и –6,00 нКл. Найти потенциал электрического поля в середине гипотенузы треугольника.

23124
По бесконечной плоскости равномерно распределенный заряд с поверхностной плотностью σ = 1 мкКл/м². На некотором расстоянии от плоскости расположен круг радиусом r = 10 см. Найти поток вектора напряженности поля Ф_Е через круг, если угол между плоскостью окружности и бесконечной плоскостью α.

24782
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ и –σ. σ = 60 нКл/м².
1. Используя теорему Остроградского-Гаусса найти выражение для напряженности Е электрического поля в трех областях: (I, II и III).
2. Вычислить напряженность Е_A в точке A, удаленной от оси цилиндров на расстояние r = 3R.
3. Построить график E(r).

25154
Тонкий жесткий диэлектрический диск радиуса R заряжен равномерно с поверхностной плотностью σ. На оси х диска на расстоянии а от его центра находится точечный заряд Q. Определить силу взаимодействия этого заряда с заряженным диском.