13459
Сплошной эбонитовый шар (ε = 3) радиусом R = 5 см заряжен равномерно с объемной плотностью ρ = 10 нКл/м³. Определите энергию электростатического поля, заключенную внутри шара.

60326
Равномерно заряженный (q = 0,3 мкКл) металлический шарик радиуса R = 0,2 м, помещен в среду с относительной диэлектрической проницаемостью ε = 3. Найти объемную плотность энергии электрического поля как функцию расстояния от центра шара.

11820
Плоская стеклянная пластинка толщиной d = 2 см заряжена равномерно с объемной плотностью ρ = 10 мкКл/м³. Найти разность потенциалов Δφ между точкой, лежащей на поверхности пластины, и точкой, находящейся внутри пластины в ее середине. Считать, что размеры пластины велики по сравнению с ее толщиной.

13032
Слой диэлектрика толщиной 25 см равномерно заряжен с объёмной плотностью заряда 12 нКл/м³. Диэлектрическая проницаемость материала слоя равна 24. Найти разность потенциалов между поверхностью слоя и его серединой.

17349
Рассчитать потенциал в центре сферы радиуса R = 0,04 м, равномерно заряженной по объему с объемной плотностью ρ = 10^–9 Кл/м².

17352
Бесконечно длинный цилиндр (внутренний радиус r = 0,05 м, внешний радиус R = 0,07 м) равномерно заряжен с объемной плотностью ρ = 4·10^–9 Кл/м³. Рассчитать напряженность электрического поля в точке, отстоящей от оси цилиндра на расстоянии S = 0,1 м.

17366
Дана бесконечно протяженная равномерно заряженная объемной плотностью ρ = 10^–5 Кл/м³ пластина толщиной d = 2 см. Найти разность потенциалов между двумя точками, лежащими вдоль одной прямой на расстояниях а = 4 см и b = 5 см от центра пластины.

17662
Шаровой слой с внешним радиусом R₁ и внутренним радиусом R₂ равномерно заряжен с объемной плотностью ρ. Напряженность электрического поля на расстоянии r от внутренней поверхности слоя (r отсчитывать в сторону центра слоя) равна 1) 0; 2) 2πkρ(R₁+r)/3(R₁²– R₂²); 3) 4πkρ(R₂+r)/3; 4) 4πkρ(R₁³–R₂³)/3(R₂+r)²; 5) 4πkρ(R₁–R₂)³/3(R₂+r)². Выбор ответа обосновать.

19200
Длинный цилиндр радиусом R равномерно заряжен с объемной плотностью ρ. Найти потенциал φ поля внутри цилиндра на расстоянии r от его оси. Принять φ(0) = 0.

19458
Равномерно заряженный шаровой слой, внутренний и внешний диаметры которого равны 2 и 4 см, притягивает точечный заряд 2 нКл, находящийся на расстоянии 5 см, с силой 2·10^–3 Н. Определить объемную плотность заряда слоя.

19550
Бесконечная пластина из диэлектрика с проницаемостью ε₁ заряжена однородно с объемной плотностью ρ. Толщина пластины равна 2а. Вне пластины ε₂ = 1. При условии, что ось X перпендикулярна пластине, и начало координат находится в середине пластины, найти Е и j внутри и вне пластины как функцию х (потенциал в середине пластины считать равным нулю). Построить графики Е(х) и j(x).

21618
Шар равномерно заряжен с объемной плотностью 0,70 нКл/м³. Найти потенциал его электрического поля как функцию расстояния от центра.

23895
Бесконечно длинный цилиндр радиуса R заряжен с объемной плотностью ρ = b/(r²+l²)^1/2, l, b — постоянные, r — расстояние от оси цилиндра. Найти E (r).

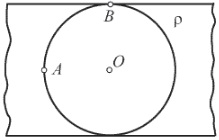
24951
В равномерно заряженной бесконечной пластине вырезали сферическую полость так, как показано на рисунке. Толщина пластины h, объемная плотность заряда ρ. Определите модуль напряженности электрического поля Е в точках А и В, а также исследуйте зависимость Е вдоль прямой ОА от расстояния X до точки О.

25005
Сферический слой радиусами R₁ = 3 см и R₂ = 5 см равномерно заряженный с объемной плотностью ρ = 3 мкКл/м³. Диэлектрическая проницаемость слоя ε₁ = 5, диэлектрическая проницаемость среды снаружи слоя (r>R₂) ε₂ = 2,5. Найти индукцию и напряженность электрического поля: в центре слоя; между поверхностями слоя на расстоянии 4 см от центра; снаружи слоя на расстоянии 4 см от наружной поверхности. Чему равна разность потенциалов между поверхностями слоя?